Es geht um die Buchreihe bzw. die Serie Game of Thrones und die inzwischen gar nicht so unrelevante Frage wann denn das nächste Buch erscheint. Kürzlich ist der Umstand eingetreten, dass die Serie dort angekommen ist wo die Bücher handlungstechnisch zur Zeit sind. Das ist so gesehen ein Novum und auch gleichzeitig eine kleine Ernüchterung für Fans – konnte man bislang doch zumindest die kleine Hoffnung hegen, dass zum Ende von Staffel fünf eventuell auch die Bucherscheinung zumindest für die absehbare Zukunft angekündigt wird. Doch nichts dergleichen. Eventuell überholt nun die Serie sogar die Bücher. Haben wir eine Möglichkeit die Frage „Wann erscheint Winds of Winter?“ (bzw. A Dream of Spring) zu beantworten? Was sind die mathematischen Hintergründe zu einer solchen Abschätzung? Und vor allem – kann diese überhaupt seriös auf diese Situation angewandt werden? Darum wird es in diesem Artikel gehen.
Das Erscheinungsdatum von Winds of Winter
Zunächst sehen wir uns an wie man überhaupt eine Möglichkeit hat Funktionen zu finden, mit denen wir auf Grundlage von bestehenden Daten aus der Vergangenheit auf zukünftige Entwicklungen zu schließen versuchen. Für Ungeduldige findet sich etwas weiter unten dann die Antwort auf die Eingangs gestellte Frage.
Im Anschluss an die Ergebnisse machen wir uns dann auch noch Gedanken darüber welche Voraussetzungen erfüllt sein müssen, damit die Seriosität einer solchen Extrapolation gewährleistet ist.
Fitten von Datensätzen
Im Artikel zur linearen Interpolation wurde das Thema Fitfunktionen schon gestreift. Grob gesagt gehts dabei darum eine Funktion gewisser Form zu finden welche einen Satz von Daten so gut wie möglich beschreibt. Im besten Fall ist die Entscheidungsgrundlage welche zur Wahl einer Fitfunktion führt ein bestehendes, gut validiertes physikalisches oder mathematisches Modell. Hier beschäftigen wir uns nun mit dem nichtlinearen Fitten von Datensätzen am Beispiel von George R. R. Martins (GRRM) Veröffentlichungsgewohnheiten bezogen auf die Hauptbuchreihe des Game of Thrones Universums.
In jedem Fall müssen wir eine ungefähre Vorstellung haben welche Form die gesuchte Funktion $f(x)$ hat – also ob es sich um ein Polynom, eine Exponentialfunktion oder ähnliches handelt.
Da wir kein physikalisches oder mathematisches Modell zu Autoren und deren Schreibgeschwindigkeit zur Verfügung haben (an dieser Stelle sollten wir bereits etwas skeptisch werden – aber darauf kommen wir am Artikelende nochmal zurück) werfen wir einen Blick darauf, wie regelmäßig George R. R. Martin bisher Bücher aus seiner Game of Thrones Serie veröffentlich hat.
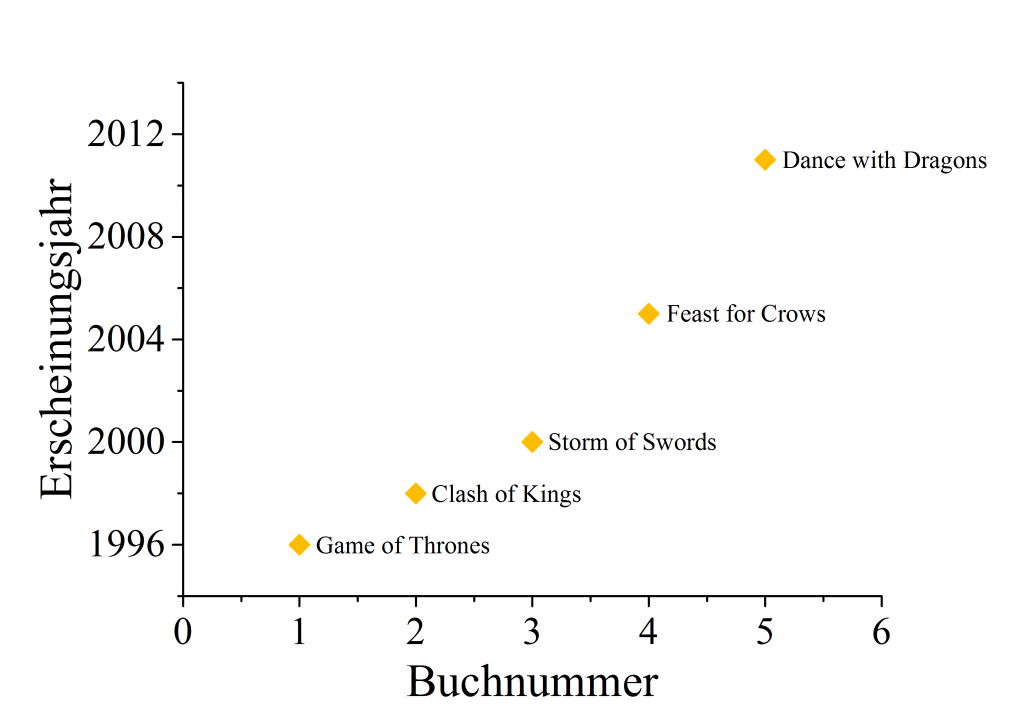
Dabei wird schnell deutlich – die Veröffentlichungsabstände stiegen bislang meistens an. Während zwischen erstem, zweitem und drittem Buch nur jeweils zwei Jahre liegen, so sind es zwischen drittem und viertem bereits fünf Jahre. Auf den zuletzt erschienenen Band Dance with Dragons mussten Fans sogar sechs Jahre warten. Wir stellen also einen nichtlinearen Anstieg der Veröffentlichungsabstände fest. Nichtlinear bedeutet dabei, dass wir Funktionen der Form
\[ f(x) = \lambda_0 + \lambda_1 x \]
eigentlich ausschließen – $x$ kommt hier nur linear vor, also nicht quadriert oder ähnliches. Exemplarisch werden wir später aber auch linear fitten. Auf die Bedeutung der $\lambda$ kommen wir ebenfalls später zu sprechen. Wir suchen jedenfalls eher etwas wie ein Polynom zweiter Ordnung
\[ f(x) = \lambda_0 + \lambda_1 x + \lambda_2 x^2 \]
oder sogar eine Exponentialfunktion:
\[ f(x) = e^{\lambda_0 + \lambda_1 x + \lambda_2 x^2 } \]
Ausgehend von dem Teil des Datensatzes den wir zur Verfügung haben wären aber eventuell noch andere Funktionen denkbar.
Fitparameter
Zunächst sollten wir uns über die Bedeutung der $\lambda$ klar werden. Unsere Eingangsdaten geben uns ja bereits x und y Punkte vor (wie in der Abbildung oberhalb geplottet):
| x (Buchnummer) | y (Jahr) | Titel |
|---|---|---|
| 1 | 1996 | Game of Thrones |
| 2 | 1998 | Clash of Kings |
| 3 | 2000 | Storm of Swords |
| 4 | 2005 | Feast for Crows |
| 5 | 2011 | Dance with Dragons |
Das bedeutet, dass die Parameter die wir optimal wählen müssen und die nicht schon vorgegeben sind eben durch alle diese $\lambda$ repräsentiert werden. Unsere gesuchte Fitfunktion $f(x)$ soll an allen so nahe wie möglich dran sein (muss sie aber nicht genau „erwischen“). Eigentlich müssten wir der Vollständigkeit halber auch immer von $f(x,\lambda_0,\lambda_1,…)$ reden, diese zusätzliche Schreibart sparen wir uns jedoch.
Weshalb ist es nicht notwendig die Eingangsdaten perfekt zu reproduzieren?
Man muss sich bei dieser Frage vor Augen führen, was solche Datensätze zumeist darstellen. Diese sind oft Messergebnisse und jede Messung ist immer mit einem gewissen Fehler behaftet. Dieser kommt dadurch zustande, dass unsere Messinstrumente nicht beliebig hohe Genauigkeit haben. Die Ergebnisse entsprechen also nie perfekt den Vorhersagen der (idealisierten) physikalischen Gesetze die das gemessene System beschreiben. Natürlich kann es vorkommen, ist aber eher unwahrscheinlich. Aufgrund dieser Umstände ist es auch nicht nur eine Frage der Notwendigkeit, sonder es ist schlicht sehr unwahrscheinlich, dass die Messdaten exakt durch unsere Fitfunktion wiedergegeben werden können.
Im Prinzip gibt es zwei Wege die gegangen werden können:
- Man kennt alle Parameter des Systems und sagt mit diesen zu erwartende Messergebnisse vorher, oder
- man betrachtet die Messergebnisse und versucht aus diesen auf nicht bekannte Parameter des System zu schließen
Fitten wir die Ergebnisse dann entspricht das sozusagen diesem zweiten Weg.
Zum Beispiel könnten wir eine Wechselspannung jede Sekunde messen (blaue Punkte in der nächsten Abbildung) und aus dem Fit dann einige Schlüsse über diese Spannung ziehen.
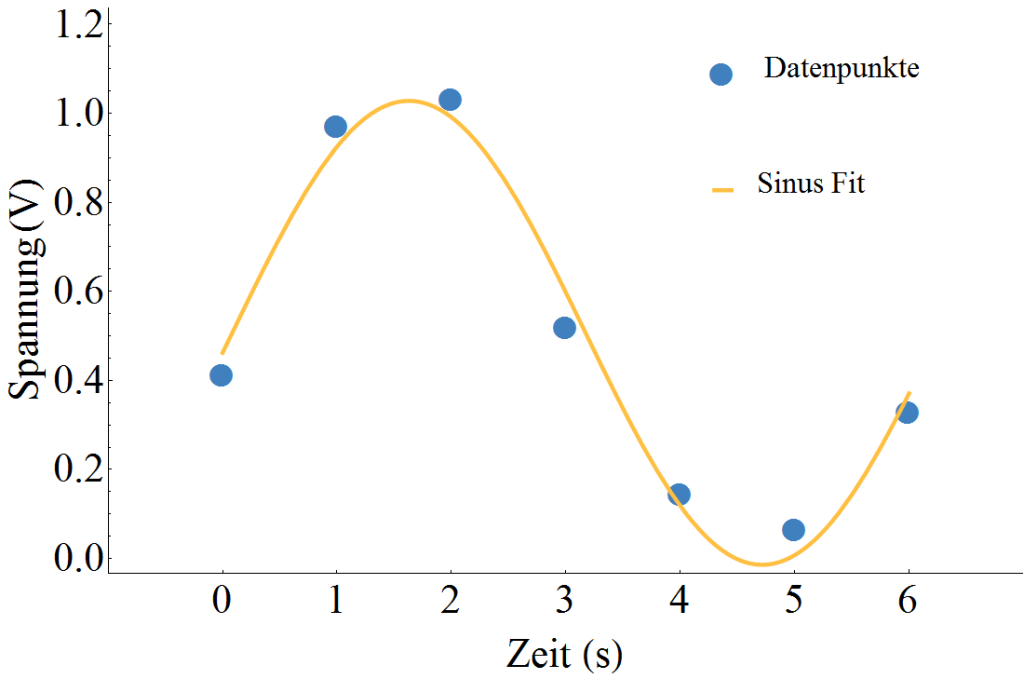
Die verwendete Fitfunktion ist in diesem Fall
\[ f(t) = \lambda_0 + \lambda_1 \sin{\left(\lambda_2 (t-\lambda_3)\right)} \]
Hierbei steht $\lambda_0$ für den Offset der Spannung, $\lambda_1$ für ihre Amplitude, $\lambda_2$ für ihre Kreisfrequenz und $\lambda_3$ für ihren zeitlichen Offset. Durch das Fitten haben wir alle Kenngrößen erhalten welche die Spannung charakterisieren (die konkreten Werte sind in der ausklappbaren Box angeführt)! Natürlich auch mit gewissem Fehler aber dennoch, damit lässt sich sehr viel anfangen.
[expand title=“Die konkreten Fitergebnisse“]
Die Ergebniswerte die wir für die Fitparameter erhalten haben sind
\[\lambda_0 = 0.51\pm 0.03\;\text{Volt} \]
\[\lambda_1=0.52\pm 0.05\;\text{Volt}\]
\[\lambda_2=1.02\pm 0.11\;\text{s}^{-1}\]
\[\lambda_3=-0.09\pm 0.09\;\text{s}\]
[/expand]
In der vorigen Abbildung wird auch deutlich, dass $f(t)$ nicht genau durch die blauen Punkte geht. Sie ist aber – unter den getroffenen Voraussetzungen – die bestmögliche Sinusfunktion die gefunden werden kann. Was bedeutet aber in diesem Fall „bestmögliche“ Wahl der Parameter? Wie bewerten wir ob eine Kuve mit $\lambda_0=0.51\;\text{Volt}$ die Spannungsmesswerte besser beschreibt als eine Kurve mit $\lambda_0=0.61\;\text{Volt}$?
Methode der kleinsten Quadrate
Wie können wir also „messen“ ob wir eine gute Wahl für alle Fitparameter getroffen haben? Ein guter Anfang ist es für jeden Punkt zu vergleichen, wie groß die Abweichung unserer Fitfunktion von den tatsächlichen Messwerten ist. Im folgenden werde ich stellvertretend für alle Fitparameter nur mehr kurz $\lambda$ schreiben.
Die Abweichung der Fitfunktion vom Messwert ist für jeden Punkt gegeben durch
\[ \Delta y_i = y_i- f(x_i,\lambda) \]
Allerdings hätten wir gerne nur eine einzige Zahl die uns einen Eindruck davon verschafft wie gut der Fit insgesamt ist. Mit obigem Vorgehen bekämen wir nur für jeden Punkt einzeln eine solche Maßzahl. Im gegenständlichen Beispiel wäre das sogar noch gut überschaubar, bei größeren Datensätzen wird man aber eher die Orientierung verlieren. Also summieren wir einfach mal über alle Differenzen auf
\[s=\sum\limits_{i=1}^{N} \Delta y_i\]
Somit hätten wir zumindest nur mehr eine einzige Zahl $s$ – leider ist diese nicht optimal. Denn die Differenz zwischen zwei Werten $\Delta y_i$ kann ja natürlich auch negativ sein. Wir können uns vorstellen, dass es Fälle gibt in denen sich Abweichungen nach oben $\Delta y > 0$ in etwa mit Abweichungen nach unten $\Delta y < 0 $ aufheben. Dann hätten wir als Ergebnis der Summe einen Wert sehr nahe oder gleich Null obwohl unsere Näherung nicht besonders gut ist. Sogar negative Werte sind für diese Summe denkbar.
Im Spannungsbeispiel wäre für $\lambda_0=0.51\;\text{Volt}$ $s=-0.02\;\text{Volt}$ bzw. für $\lambda_0=0.61\;\text{Volt}$ ergäbe sich $s=-0.72\;\text{Volt}$. Beides ist nicht sehr aussagekräftig!
Die Lösung – um solche Probleme zu vermeiden – ist den Term $\Delta y_i$ zu quadrieren. Somit summieren wir nur positive Werte und vermeiden die zuvor beschriebene Problematik. Um so größer das Ergebnis der Summe, um so schlechter der Fit! Außerdem hat das quadrieren noch einen zusätzliche sehr angenehme Nebenwirkung – kleinere Abweichungen wirken sich weniger stark aus als große. Sehr nützlich wenn wir bewerten wollen wie gut unsere Näherung ist.
\[ S=\sum\limits_{i=1}^{N} (y_i – f(x_i,\lambda))^2 \]
Damit erhalten wir also eine Maßzahl dafür, wie gut eine Fitfunktion gemessene Datenpunkte annähert. Wie sieht das nun für das Spannungsbeispiel aus?
Hier berechnen wir für $\lambda_0=0.51\;\text{Volt}$ ein Ergebnis der Summe von $S=0.02\;\text{Volt}^2$ und für $\lambda_0=0.61\;\text{Volt}$ ist $S=0.09\;\text{Volt}^2$. Ganz klar, erstere Wahl für $\lambda_0$ liefert kleinere Abweichungen. Die Einheiten hängen natürlich vom konkreten Beispiel ab – da es in unserem Fall um Spannungen geht ist dies das Volt.
Wollen wir also einen guten Fit finden müssen wir sämtliche $\lambda$ so wählen, dass der Wert von $S$ so klein wie möglich wird. Daher auch der Name: Methode der kleinsten Quadrate. Für lineare Fits gibt es dabei exakte Lösungen, bei nichtlinearen sind dazu numerische Berechnungen notwendig.
Jetzt wissen wir, wie entschieden werden kann, welche Fitparameter „die Besten“ sind. Kommen wir also auf die ursprüngliche Fragestellung bezüglich der Erscheinungsjahre zurück. Um diese zu beantworten habe ich drei verschiedene Fits durchgeführt, einen lineareren Fit, einen polynomialen Fit zweiter Ordnung und einen exponentiellen Fit. Die genauen Ergebnisse, Fehler in den Fitparametern und Gleichungen finden sich in der folgenden Tabelle.
| Name | Fitfunktion | $\lambda_0$ | $\lambda_1$ | $\lambda_2$ | $S$ |
|---|---|---|---|---|---|
| linearer Fit | $\lambda_0 + \lambda_1 x$ | $1991\pm 2$ | $3.7\pm0.6$ | - | $9.2$ |
| Polynom 2. Ordnung | $\lambda_0 + \lambda_1 x + \lambda_2 x^2$ | $1996\pm 1$ | $-1\pm 0.8$ | $0.8\pm 0.1$ | $0.76$ |
| Exponentialfunktion | $e^{\lambda_0 + \lambda_1 x + \lambda_2 x^2}$ | $7.599\pm 0.0001$ | $(-5\pm 4) 10^{-4}$ | $(3.9 \pm 0.6) 10^{-4}$ | $0.69$ |
Aus den Werten für $S$ können wir schließen, dass der Fit mit der Exponentialfunktion die Veröffentlichungsjahre am besten beschreibt. Nun verwenden wir diesen um in die Zukunft zu extrapolieren – wann erscheinen die verbleibenden beiden Bücher?
Wann erscheint Winds of Winter?
Der exponentielle Fit legt ein Erscheinen von The Winds of Winter Mitte 2018 nahe. Mit dem Abschluss der Reihe, A Dream of Spring, wäre dagegen erst Ende 2027 zu rechnen.
Wie gut sind nun diese Ergebnisse?
Es gibt verschiedene Gründe warum man solcherart Resultate nicht ernst nehmen sollte. Ein ganz guter erster Indikator bezüglich Seriosität ist, ob für die Abschätzung angegeben wurde wie groß ihre Schwankungsbreite ist.
Die Schwankungsbreite
Wir kennen ja die Fehler in den Fitparametern – mit dem Gauß’schen Fehlerfortpflanzungsgesetz können wir eine erste grobe Abschätzung durchführen, wie sehr diese Ungenauigkeiten sich auf das Endergebnis auswirken.
Es zeigt sich, dass der exponentielle Fit auch gleichzeitig der ungenaueste ist, der Fehler für das Erscheinungsdatum von Winds of Winter beträgt fast sieben Jahre! Ob es lt. Ergebnis jetzt Mitte oder Ende des Jahres erscheint geht bei dieser Schwankungsbreite völlig unter. Auch wird schnell deutlich, dass die Vorhersage schon nur mehr eingeschränkt relevant ist: Der Fehler ist größer als alle Abstände zwischen den Büchern bisher. Es klingt halt nicht mehr sooo spannend wenn man sagt „Das Buch erscheint $2018\pm 7$ Jahre.
Für a Dream of Spring wächst der Fehler schließlich sogar noch weiter an. Die folgende Tabelle beinhaltet eine Übersicht.
| Buch | Fitfunktion | Erscheinungsjahr |
|---|---|---|
| The Winds of Winter | linear | $2013 \pm 4$ |
| polynomial | $2019 \pm 6$ | |
| exponential | $2018 \pm 7$ | |
| A Dream of Spring | linear | $2017 \pm 4$ |
| polynomial | $2028 \pm 8$ | |
| exponential | $2028 \pm 8$ |
Kein zugrundeliegendes Modell
Dann kommt noch ein weiterer Fallstrick hinzu. Es gibt keinen Grund anzunehmen, dass sich das Veröffentlichungsdatum tatsächlich mit einer der oben verwendeten Funktionen darstellen lässt. Im Fall der Wechselspannung ist dies anders, es existiert ein physikalisches und bestens validiertes Modell. Wechselspannungen können in sehr guter Näherung durch eine Sinusfunktion beschrieben werden. Die Schreibgeschwindigkeit eines Autors hingegen? Hier gibt es keine argumentierbare Grundlage dafür anzunehmen, dass die Veröffentlichungsabstände immer größer werden. Zumindest meines Wissens nach existiert kein mathematisches oder physikalisches Modell dazu.
Die Anzahl der Datenpunkte
Ein Blick auf die erste Abbildung dieses Artikels die nicht GRRM zeigt (also die mit den Veröffentlichungsjahren der Bücher) sagt uns, dass wir es eigentlich mit sehr wenigen Datenpunkten zu tun haben. Um einen aussagekräftigen Fit zu erhalten möchte man eigentlich, dass die Anzahl de Datenpunkte viel größer ist, als die Anzahl der Fitparameter. In unserem Fall stehen nur fünf Datenpunkte bis zu drei Fitparametern gegenüber. Das ist tatsächlich ein schlechtes Verhältnis und ein weiteres Warnsignal wenn es um die Qualität der Ergebnisse geht. (Dank an Philippe Seil für den Hinweis).
Fehler in der Annahme und ein Zirkelschluss
Noch ein weiteres vielleicht nicht so offensichtliches Problem verbirgt sich in alledem. Wir konnten zwar bis jetzt beobachten, dass die zeitlichen Abstände zwischen Büchern immer größer werden, aber wir wissen eigentlich nicht ob es auch in Zukunft so sein wird. In die Auswahl der Fitfunktionen ist aber bereits diese Voreingenommenheit mit eingeflossen – wir haben eine Funktion gewählt die immer konstant ansteigt, und welche die immer stärker ansteigen. Weshalb haben wir keine gewählt, welche nach Buch fünf wieder flacher steigt? So gesehen erhalten wir als Ergebnis etwas, dass wir bereits in die Analyse mit hineingesteckt haben. Ein Zirkelschluss also.
Fitfunktionen sind also, sofern kein mathematisch / physikalisches Modell hinter den Daten steckt, ebenfalls nicht ohne eine gewisse Vorsicht anzuwenden.
Alles in allem ist die konkrete Fragestellung – Wann erscheint The Winds of Winter oder Wann erscheint A Dream of Spring zwar ein nettes Rechenbeispiel wenn man versucht sie mit Fitting Methoden zu beantworten, aussagekräftig ist die Antwort allerdings aus genannten Gründen nicht. Aber es ist eine gute Gelegenheit, sich über Methoden die regelmäßig und häufig verwendet werden etwas mehr Gedanken zu machen. Nebenbei überbrückt man auch die Wartezeit aufs nächste Buch etwas…
Editierungen
- 16.07.2015 – Vielen Dank an Philippe Seil für den Hinweis darauf, dass beim ersten Vorkommen der quadratischen Fitfunktion das Quadrieren der entsprechenden unabhängigen Variable vergessen wurde und den Hinweis, dass auch die Anzahl der Datenpunkte viel größer sein sollte als die Zahl der Fitparameter um einen aussagekräftigen Fit zu erhalten.
![By User:dravecky (Own work) [CC BY-SA 3.0], via Wikimedia Commons](/wp-content/uploads/2015/06/1280px-George_R._R._Martin_signing_at_LoneStarCon3.jpg)
Ein Kommentar