Interpolationsmethoden – Lineare Interpolation

In diesem Artikel geht es darum wie lineare Interpolation in ein und zwei Dimensionen funktioniert, und andererseits darum, weshalb man sich gut überlegen sollte ob man Datenpunkte tatsächlich interpolieren möchte. In anderen Bereichen hat Interpolation natürlich auch ohne „Wenn und Aber“ eine Daseinsberechtigung, so liefert sie eine Methode wie zum Beispiel Bilder skaliert werden können.

Wozu gibts die Interpolation?

In erster Linie steht man irgendwann einmal vor der Situation ein paar Datenpunkte vor sich zu haben.

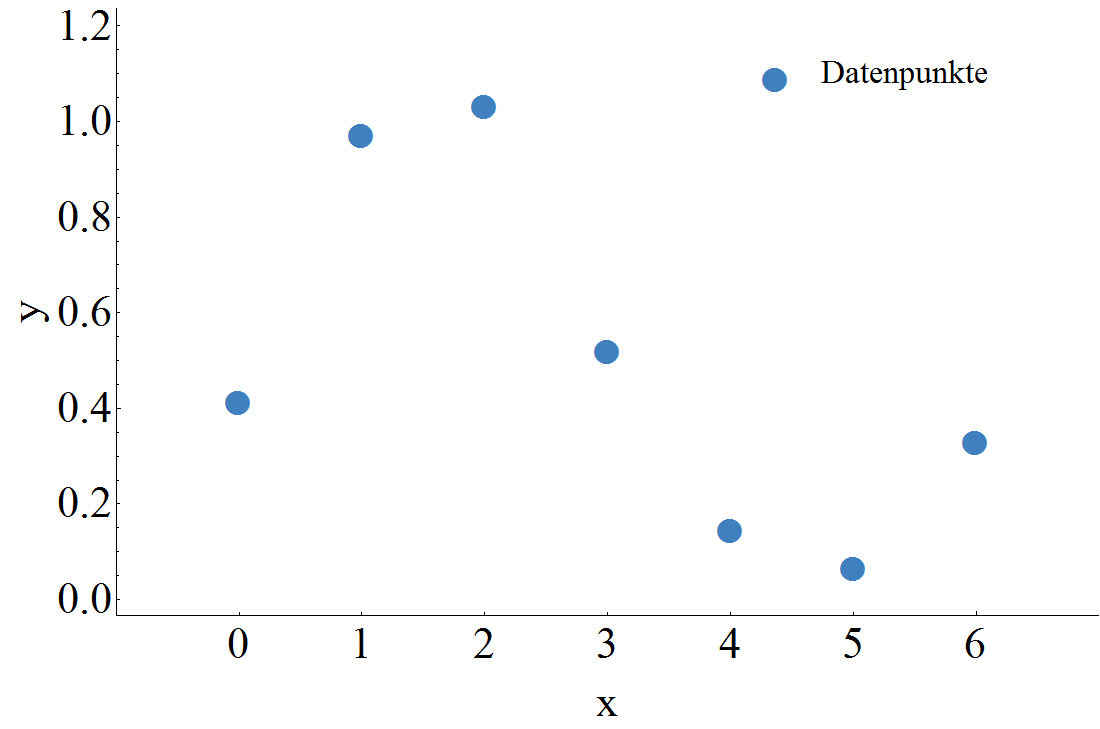
Diese Datenpunkte könnten den Zeitverlauf einer Wechselspannung $U(t)$ repräsentieren, es könnte aber auch die Helligkeitsschwankung entlang der x Koordinate eines Bildes sein.

Die genaue formale Abhängigkeit $g(x)$ ist oft nicht bekannt, vielleicht auch einfach zu aufwendig um direkt implementiert zu werden oder existiert, wie zum Beispiel im Fall der Bildskalierung, schlichtweg nicht. Was gibt es für Möglichkeiten wenn nun dennoch – in obigem Fall zum Beispiel – $g(1.5)$ gesucht ist? Interpolationsmethoden sind eine mögliche Antwort.

Bevor wir uns allerdings auf diese stürzen nehmen wir uns etwas Zeit. Denn sobald es um Messdaten geht gilt: Vorsicht mit Interpolationsfunktionen!

Achtung bei Messdaten!

Gleich vorweg eine „Warnung“ für alle die Daten aus Messungen interpolieren wollen: Während Interpolation auch bei einer physikalischen Interpretation des Messdaten sinnvoll sein kann, stellen Fitfunktionen in den meisten Fällen wohl die bessere Wahl dar.

Eine physikalische Interpretation wäre für obige Abbildung eben eine Wechselspannung $U(t)$. Diese lässt sich durch $U(t) = y_0 + A \sin{\left(\omega (t-t_0)\right)}$ beschreiben. Eine Fitfunktion würde nun jene Amplitude $A$, Frequenz $\omega$ und Offsets $y_0$, $t_0$ aufweisen, welche insgesamt zu geringstmöglicher Abweichung von den Datenpunkten führen. Dabei ist es nicht notwendig, dass die Fitfunktion auch exakt durch die Datenpunkte verläuft!

Eine Interpolationsfunktion $f(x)$ ist hingegen eine rein mathematische Methode um Datenpunkte zu verbinden. Es gibt aufgrund dieses Vorgehens im Allgemeinen keinen Zusammenhang zwischen $f(x)$ und einer Messung des Parameters auf den Verbindungsstücken. Diese können zufälligerweise übereinstimmen, müssen es aber nicht.

Das bedeutet natürlich nicht, dass die Fitfunktion zwangsläufig bessere Ergebnisse liefert, aber in ihrem Fall ist es durch eine physikalische Theorie argumentierbar weshalb man erwartet, dass eine vorgenommene Messung ähnliche Werte liefern würde! In der folgenden Abbildung findet sich eine Gegenüberstellung zwischen einer Fitfunktion und einer einfachen Interpolationsmethode – der linearen Interpolation – für obige Datenpunkte.

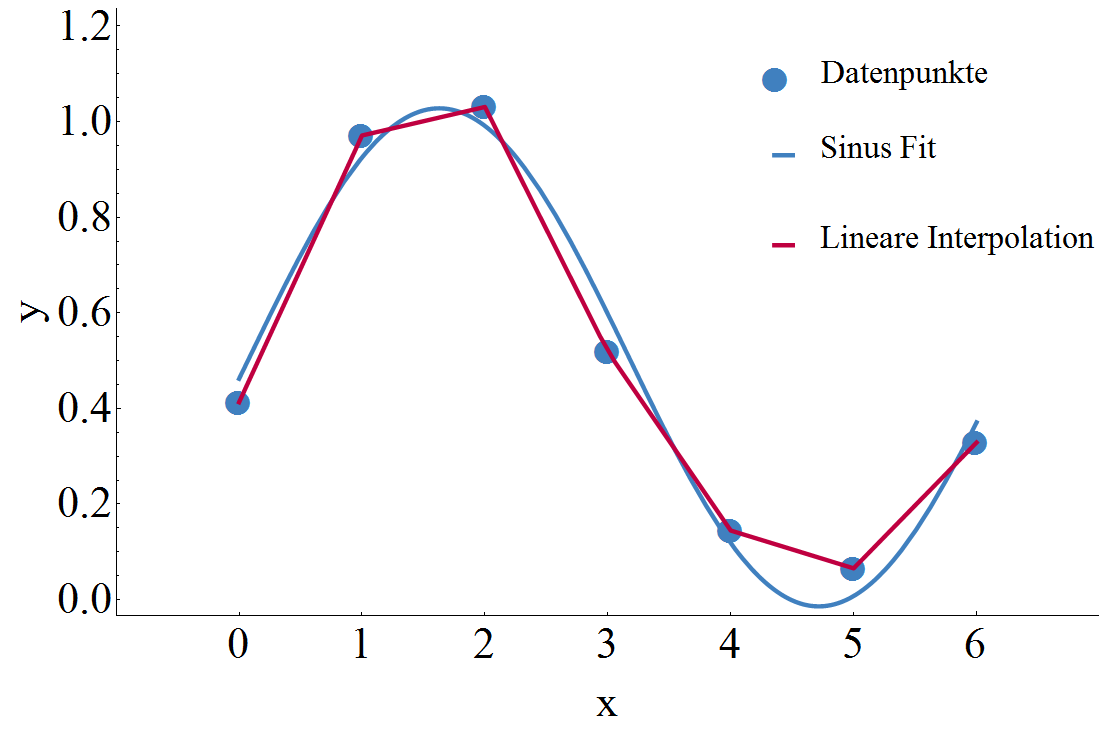
Abgesehen vom bisher Genannten kann das übereifrige Verwenden von Interpolationsfunktionen noch zu ganz anderen Problemen führen.

Eine Frage der Suggestion

Tabellenkalkulationsprogramme wie Excel verleiten besonders dazu unhinterfragt Interpolationsfunktionen zu verwenden. Diese sehen zwar oft „hübsch“ aus, bringen jedoch keinen Mehrwert und können die Interpretation von Daten sogar erschweren. Die Verbindungslinien zwischen den Punkten suggerieren nämlich, dass dazwischen „alles wie erwartet“ verläuft. Unser Auge wird fließend von Punkt zu Punkt geleitet und alles sieht schön glatt aus. Es bildet sich rein durch die Betrachtung eine Annahme darüber was bei den Verbindungsstücken passiert, und das obwohl es dafür keine Rechtfertigung gibt!

Im Fall von Fitfunktionen ist man zwangsläufig damit beschäftigt die Daten zu interpretieren und ein theoretisches Modell anzuwenden. Führt der Fit einfach zu keinem guten Ergebnis deutet dies mitunter schon an, dass das Modell oder die getroffenen Annahmen vielleicht nicht so gut passen wie gedacht – oder die Daten vielleicht nicht so viel hergeben wie man gerne hätte.

In jedem Fall läuft man – wenn es um Messdaten geht – bei der Verwendung von Interpolationsfunktionen Gefahr durch ein hübsches Bild etwas zu suggerieren, was nicht da ist. Um nicht diesen Eindruck zu erwecken findet sich in Papers manchmal der Hinweis, dass man damit keine physikalische Interpretation anstrebt, sondern nur Überblick schaffen möchte.

Um das ein bisschen besser zu beleuchten betrachten wir ein Beispiel dafür wie Interpolation auf eine falsche Fährte führen kann.

Fehlschlüsse durch Interpolation

Betrachten wir die Daten die uns eine meteorologische Station liefert. Wir sehen uns hierfür die Globalstrahlungsmessdaten für einen Sommertag an. Die Globalstrahlung $G$ ist dabei die Intensität jener Strahlung die uns aus dem gesamten Himmel erreicht. Also die direkte Sonnenstrahlung plus die Diffuse Strahlung des Himmels (das „Himmelsblau“ sozusagen). Genauer gesagt misst die Wetterstation die Energie die innerhalb einer Stunde durch die Strahlung auf eine horizontale Messfläche deponiert wird.

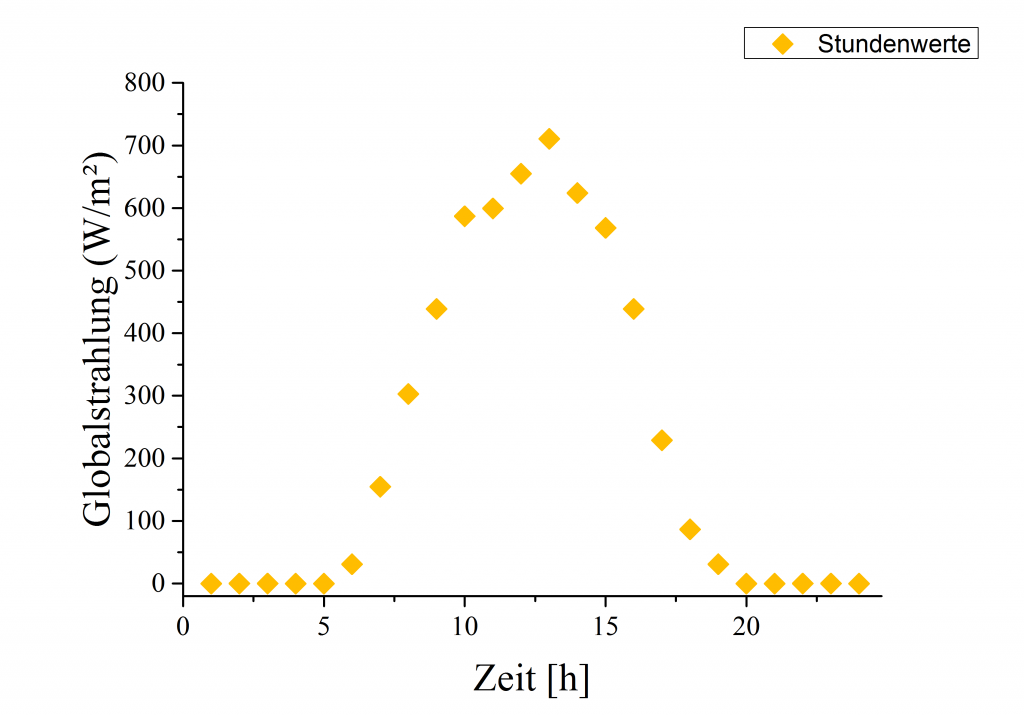
Daraus ergibt sich das obige Bild. Wir stellen fest, dass mit dem Sonnenaufgang die Strahlung stark ansteigt, scheinbar um die Mittagszeit ihren Höhepunkt erreicht, und bis zum Sonnenuntergang wieder abnimmt.

Stellen wir nun die Frage wieviel Globalstrahlung $G$ um 11:30 die Messfläche erreicht haben müsste. Da wir nur die Messwerte für volle Stunden zur Verfügung haben müssen wir einen Weg finden um dennoch einen vernünftigen Wert zu erhalten. Eine physikalische Interpretation auf dem Weg zu einer Fitfunktion wäre möglich, allerdings mit nicht unerheblichem Aufwand verbunden – daher entscheiden wir uns für eine Interpolationsfunktion. In Excel würde beispielsweise automatisch entweder linear oder mit Splines interpoliert. Das ergäbe den folgenden Plot:

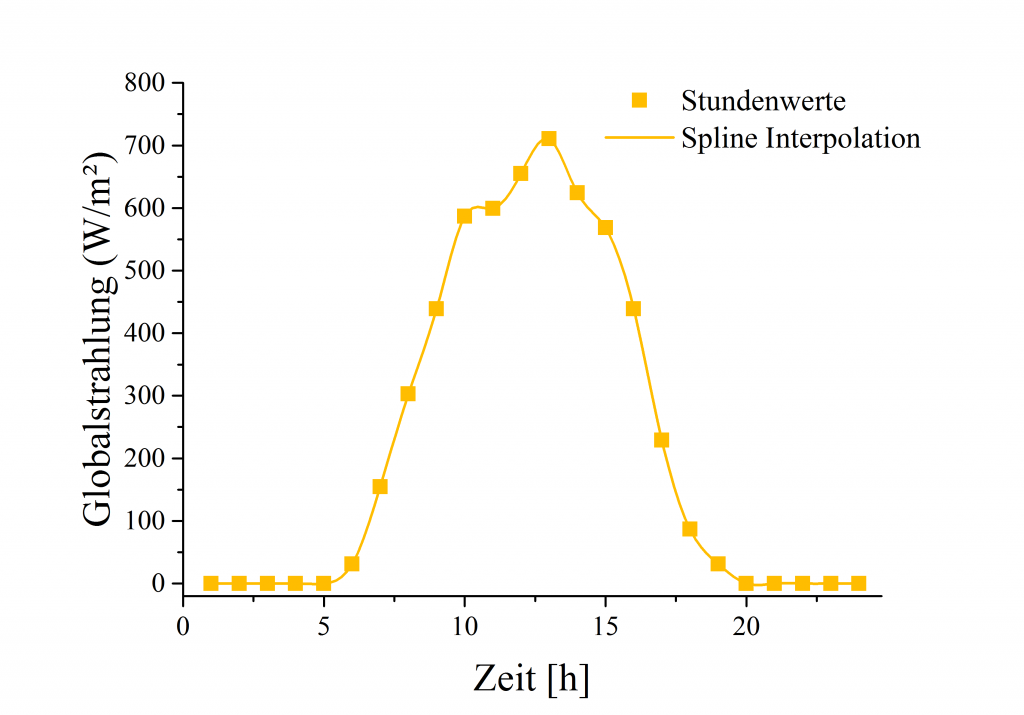
Nun können wir den Spline für $t=11.5\text{h}$ auswerten und erhalten ca $620\;\text{W/m}^2$. Werfen wir nun aber einen Blick auf denselben Tag nur mit einer besseren Zeitauflösung:

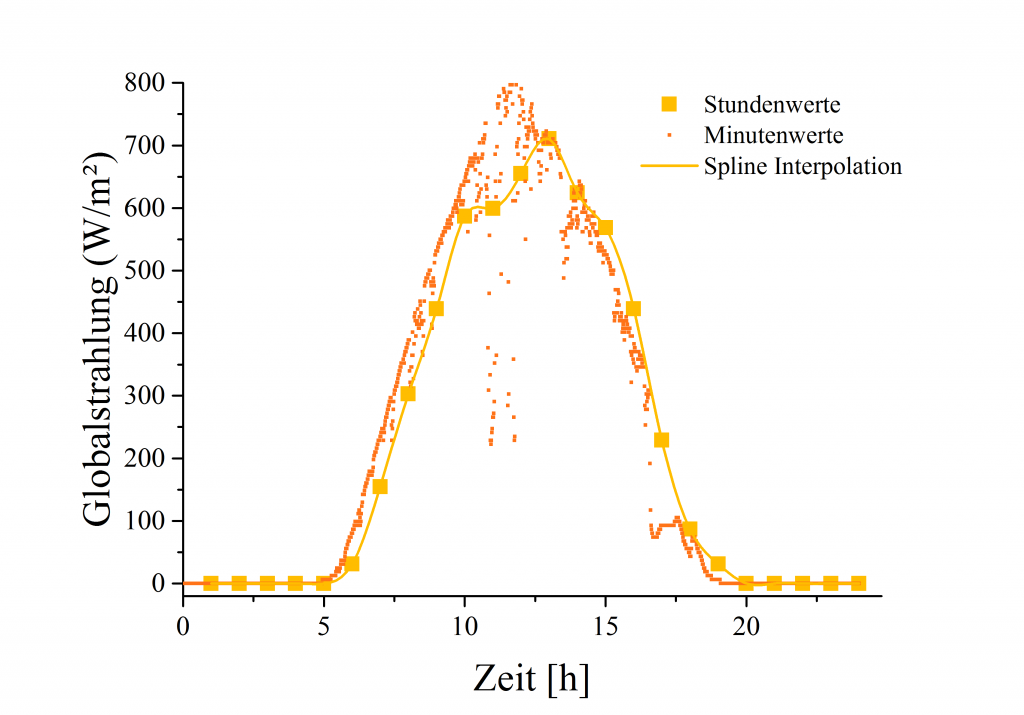
Wir erkennen sehr schnell, dass der Spline irreführend ist. Wir haben zuvor ja festgestellt, dass die Datenpunkte im Prinzip der mittleren Strahlungsintensität während jeder Stunde entsprechen (dh. der Datenpunkt für 07:00 entspricht dem Mittel von 06:01 bis 07:00). Das impliziert auch, dass es in diesen Intervallen natürlich auch zu Schwankungen nach oben und unten kommen kann. Es scheint als ob an diesem Sommertag um die Mittagszeit, zu der auch die höchste Globalstrahlung auftritt, hin und wieder Wolken die Sonne blockiert haben. Daher die tieferliegenden Minutenwerte in diesem Zeitraum. Allerdings werden diese durch die wolkenfreien Phasen teilweise wieder ausgeglichen, sodass die Stundenwerte in etwa zwischen $600-700\;\text{W/m}^2$ liegen.

Zusätzlich liegen während des Vormittags (05:00 bis ca. 12:00) die Stundenwerte unterhalb der Minutenwerte, für den Nachmittag liegen sie aber darüber. Einfach als Konsequenz der Messmethodik.

Während der Spline für 11:30 einen Wert von $620\;\text{W/m}^2$ lieferte, ergeben die Minutenwerte $G(11.5)=780\;\text{W/m}^2$! Der Spline liegt also immerhin $20\%$ darunter.

Natürlich kommt es nun darauf an, wofür der Wert benötigt wird. Ist tatsächlich der momentane Wert zu diesem Zeitpunkt gefragt, gibt es eventuell einfach keine bessere Möglichkeit als zu interpolieren. Allerdings darf dabei nicht auf die physikalische Interpretation vergessen werden (in diesem Fall: Wolken könnten zu Fluktuationen führen die nicht im Mittelwert feststellbar sind) und man müsste auf eine vernünftige Art und Weise abschätzen, wie groß der Fehler der durch den Spline (oder die Interpolationsfunktion) ermittelten Größe sein kann.

Grundsätzlich möchte ich hier auch nicht gegen Interpolationsfunktionen wettern, aber ich denke doch, dass es wichtig ist darauf hinzuweisen, dass man bei ihrer Verwendung diese Probleme immer im Hinterkopf haben sollte. Wichtig ist, und das auch unabhängig davon ob man interpoliert, dass man nicht vergisst, was sich hinter den Datenpunkten verbirgt: Die Interpretation, die Messtechnik, etc.

Aber jetzt nach alledem können wir damit starten, wie man denn eigentlich linear interpoliert – weiter gehts aus der nächsten Seite!