Was bisher geschah
Inzwischen haben wir in dieser Artikelserie ja einiges über Infrarotkameras gelernt. Wir kennen die zugrunde liegende Idee und die Methode die zur Temperaturbestimmung angewandt wird. Dann haben wir einen ersten Schritt von der idealisierten Welt in die reale Welt getan und den Emissionskoeffizienten als wichtigen Parameter entdeckt. Zum Schluss wollen wir nun etwas genauer nachvollziehen, wie man von einem Signal am Detektor mit Hilfe der Messgleichung letztlich auf eine Temperatur kommt.
Inhalt der Artikelserie
Teil 1 – Grundlegendes
Teil 2 – Temperaturbestimmung
Teil 3 – Emissionskoeffizient
Teil 4 – Die Messgleichung
Warum das überhaupt wichtig ist
Das Prinzip verstehen wir ja bereits, weshalb jetzt noch eine Gleichung? Nun ja, überlegen wir kurz nochmal was bei einer Messung eigentlich passiert.
Strahlung trifft am Detektor ein und verursacht dort ein Signal mit gewisser Stärke. Aber wo kommt die Strahlung her? Von dem Objekt dessen Temperatur wir bestimmen möchten. Das kann man zwar so stehen lassen, aber man läuft Gefahr ein paar wichtige Subtilitäten zu übersehen wenn man nicht genauer hinsieht.
Langwellige elektromagnetische Strahlung ist ja nichts anderes als Licht dass wir (eigentlich) nicht wahrnehmen können weil unsere Augen keine entsprechenden Rezeptoren aufweisen. Licht kann aber auch reflektiert werden und nur deswegen sehen wir die Objekte die nicht von sich aus Licht abgeben. Aber Reflektion kommt natürlich auch im gesamten elektromagnetischen Spektrum vor, also auch im infraroten Teil davon.
Dies bedeutet, dass ein Teil der Strahlung welche an der Kamera ankommt nicht vom Objekt unseres Interesses abgegeben wurde sondern dort einfach nur reflektiert wurde. Das ist allerdings immer noch nicht alles. Zwischen Kamera und Objekt befindet sich Luft. Und Luft kann – abhängig von der Luftfeuchtigkeit – ebenfalls Strahlung emittieren. Das ist zwar nicht so viel, aber wenn ausreichend viel Distanz zwischen Kamera und Objekt ist dann kann sich das schon aufsummieren.
Aber Luft hat aus einem anderem Grund noch Einfluss: Elektromagnetische Strahlung wird, während sie sich durch Luft fortbewegt, abgeschwächt. Diese Abschwächung wird durch das Lambert-Beer Gesetz beschrieben.
Wie können wir nun herausfinden was tätsächlich vom Objekt kommt und was nur reflektiert oder von der Luft abgegeben oder absorbiert wurde? Damit beschäftigen wir uns in den nächsten Absätzen.
Wieviel Strahlung tatsächlich vom Objekt kommt
Zuerst können wir das Ganze mal in Form einer Gleichung anschreiben um einen Überblick zu bekommen. Das Signal am Detektor setzt sich also aus drei Anteilen zusammen
\[ S_\text{Gesamt} = S_\text{Objekt} + S_\text{Reflektiert} + S_\text{Luft} \]
Die Signalstärke $S$ ist dabei im Prinzip proportional zur Strahlungsleistung die sie verursacht. Also $S \approx k \; P$. Das ist recht praktisch denn es erleichtert uns die Umformung.
\[P_\text{Gesamt} = P_\text{Objekt} + P_\text{Reflektiert} + P_\text{Luft} \]
Das hätten wir auch erwartet – die Gesamtstrahlung die bei der Kamera ankommt ist die Summe aus den drei zuvor beschriebenen Teilen. Also $P_\text{Objekt}$ der Teil der vom Objekt selbst abgegeben wird, $P_\text{Reflektiert}$ jene EM Strahlung die aus der Umgebung kommt und am Objekt zu uns hin reflektiert wird und $P_\text{Luft}$ schließlich die Strahlung, die von der Luft noch abgegeben wird. Formen wir zuerst einfach mal nach $P_\text{Objekt}$ um:
\[P_\text{Objekt} = P_\text{Gesamt} – P_\text{Reflektiert} – P_\text{Luft} \]
Wir kennen zur Zeit nur $P_\text{Gesamt}$ – das misst die Kamera ja. Wenn wir dann noch den Beitrag der reflektierten Strahlung abziehen können und auch noch den Lufteinfluss weg subtrahieren, dann haben wir das was uns eigentlich interessiert. Aus $P_\text{Objekt}$ lässt sich dann gut die Temperatur bestimmen, welche eine solche Strahlungsleistung verursachen würde.
Um weiter machen zu können beschäftigen wir uns nun damit, was mit Strahlung alles passieren kann wenn sie bei einem Objekt ankommt. Das wird uns im nächsten Schritt dann helfen.
Absorption, Emission, Transmission und Reflektion
Ein paar Dinge hatten wir schon erwähnt ohne genau darauf einzugehen. Hier sind sie nochmals zusammengefasst. Stellen wir uns vor, was mit einem Lichtstrahl der auf ein Objekt trifft passieren kann.
Ein Teil des Lichts wird an der Oberfläche reflektiert werden, ein anderer Teil wird in das Objekt eindringen und transmittiert (wie zum Beispiel sichtbares Licht durch Glas). Aber passiert der Strahl das Objekt verlustfrei? Nein, ein gewisser Anteil wird absorbiert. Je weiter die zurückgelegte Strecke ist, desto mehr wird insgesamt absorbiert werden.
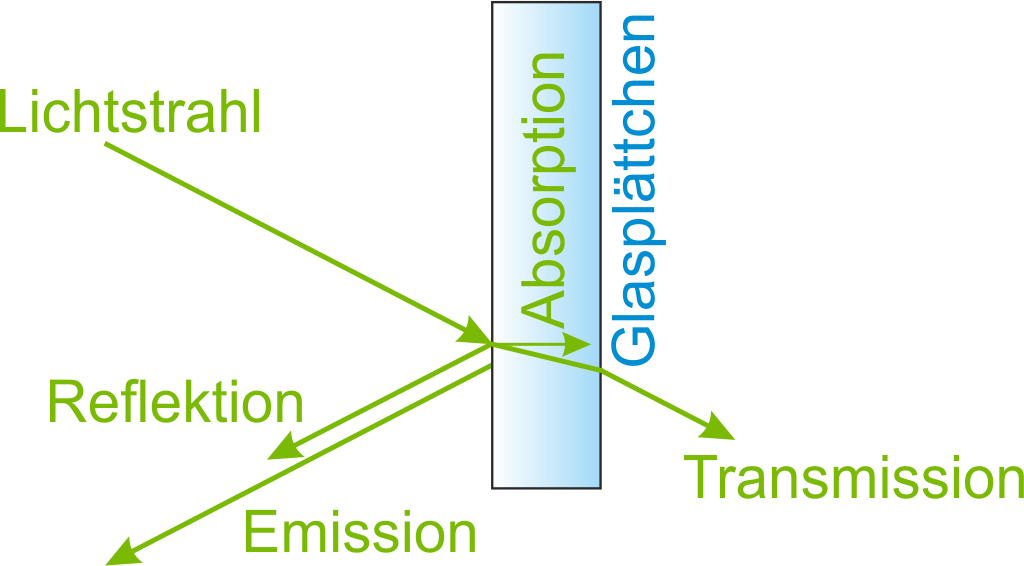
Es gibt für unseren Lichtstrahl an der Oberfläche des Glasplättchens also drei Möglichkeiten: Reflektion $r$, Transmission $\tau$ und Absorption $a$ und daher gilt
\[ 1= r + \tau + a \qquad \qquad (1)\]
Emission berücksichtigen wir hier nicht mit da wir nur die Möglichkeiten betrachten die es für einen einfallenden Lichtstrahl gibt, der Vollständigkeit halber ist dies aber in obiger Abbildung dennoch eingezeichnet. Letztlich ist diese Gleichung jedenfalls aus der Energieerhaltung ableitbar. Anschaulich hat der ursprüngliche Lichstrahl eine gewisse Intensität $I_0$ und diese teilt sich entsprechend der drei Prozesse auf. Ein Teil wird absorbiert $I_\text{absorbiert}$, ein weiterer reflektiert $I_\text{reflektiert}$ und ein weiterer transmittiert $I_\text{transmittiert}$. Natürlich kann die Summe dieser drei Teile nicht größer oder kleiner sein, als die ursprünglich zur Verfügung stehende Intensität!
\[ I_0 = I_\text{reflektiert} + I_\text{transmittiert} + I_\text{absorbiert}\qquad (2) \]
Das Verhältnis zwischen reflektierter und Ursprünglicher Intensität bezeichnen wir nun als Reflektionskoeffizient
\[ a= \frac{I_\text{absorbiert}}{I_0}, \quad \tau= \frac{I_\text{transmittiert}}{I_0}, \quad r = \frac{I_\text{reflektiert}}{I_0}\]
und entsprechend gehen wir für die beiden anderen Teilintensitäten vor.
Dividiert man nun Gleichung (2) durch $I_0$ bleibt links des Gleichheitsszeichens $1$ übrig und rechts die entsprechenden Koeffizienten.
So weit so gut.
Schritte zur Messgleichung
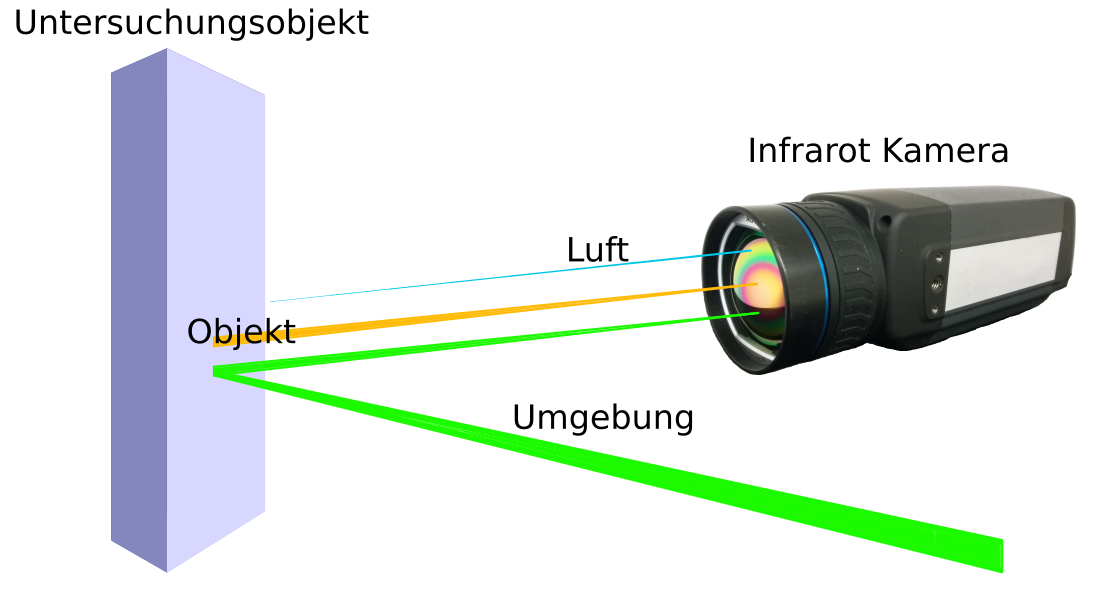
Das Ziel hier ist einmal ausführlich anzuschreiben, von welchen Parametern die Gesamtstrahlung die bei der Kamera eintrifft abhängt. Dazu wiederholen wir eine eingangs angeschriebene Gleichung:
\[P_\text{Gesamt} = P_\text{Objekt} + P_\text{Reflektiert} + P_\text{Luft} \qquad \qquad (3) \]
Die Strahlungsleistung die bei der Kamera insgesamt eintrifft ist die Summe der Strahlung die vom Untersuchungsobjekt ausgeht $P_\text{Objekt}$, der durch die Luft zwischen Kameraobjektiv und Versuchsobjekt abgegebenen Strahlung $P_\text{Luft}$, und der aus der Umgebung kommenden am Versuchsobjekt reflektierten Strahlung $P_\text{Reflektiert}$.
Zunächst aber noch eine Erinnerung: Die durch einen schwarzen Körper abgegebene Strahlungsleistung ist
\[P(T) = \sigma A T^4 \]
mit $\sigma = 5.67 \cdot 10^{-8}$ als die Stefan-Boltzmann Konstante. Das ist der Brückenschluss zu einem weiteren Artikel in dieser Serie, denn das Stefan-Boltzmann Gesetz ergibt sich, wenn man das Planck’sche Strahlungsgesetz über alle Frequenzen und den gesamten Halbraum integriert. Es gibt also die Strahlungsleistung an, die ein schwarzer Körper der Temperatur $T$ und Oberfläche $A$ über den gesamten Frequenzbereich in den Raum abstrahlt.
Strahlungsleistung des Versuchsobjekts
Um den ersten Term der Messgleichung zu erhalten, verwenden wir ein paar Dinge, die wir im letzten Eintrag dieser Serie gelernt haben. Zum Beispiel nehmen wir an, dass sich unser Untersuchungsobjekt wie ein grauer Körper mit Emissionsgrad $\epsilon_O$ verhält. Außerdem berücksichtigen wir, dass nur ein Teil der Strahlung zwischen Infrarotkamera und Versuchsobjekt von der dazwischen liegenden Luft transmittiert wird. Die vom Objekt abgegebene Strahlungsleistung die bei der Kamera ankommt ist dann gegeben durch
\[P_\text{Objekt} = \tau_L \, \epsilon_O P(T_O). \]
Hierbei steht $\epsilon_O$ für den Emissionskoeffizient des Objekts, $T_O$ für dessen Oberflächentemperatur und $\tau_L$ für den Transmissionskoeffizienten von Luft.
Reflektierte Strahlungsleistung aus der Umgebung
Auf ähnliche Weise können wir uns überlegen, wie wir die am Untersuchungsobjekt reflektierte Strahlung die aus der Umgebung kommt quantifizieren. Mit Umgebung ist hier tatsächlich das Umfeld in dem wir unsere Messung durchführen gemeint. Das kann das Labor sein oder ein offenes Feld mit klarem oder bewölktem Himmel. Hier ist die Strategie so, dass wir die Umgebung näherungsweise als schwarzen Körper der Temperatur $T_U$ beschreiben. Auch ist erneut relevant, dass nicht alle Strahlungsleistung durch dazwischenliegende Luft transmittiert wird sondern nur ein Bruchteil davon. Wir erhalten:
\[ P_\text{Reflektiert} = \tau_L \, r_O \, P(T_U) \]
Hier ist $\tau_L$ die Transmissivität der Luft und $r_O$ die Reflektivität der Oberfläche unseres Versuchsobjektes. Zumeist wird dieser Term noch weiter umgeformt um nicht extra $r_O$ abschätzen oder ausrechnen zu müssen. Von unserem Versuchsobjekt wird angenommen, dass es keine Infrarotstrahlung durchtreten lässt, also $\tau_O = 0$. In Gleichung (1) eingesetzt und nach $r_O$ umgeformt ergibt dann, dass $r_O = 1-a_O$. Schließlich machen wir uns noch das Kirchhoff’sche Strahlungsgesetz zu Nutze (auf das wir aber vorerst nicht weiter eingehen). Dieses besagt, dass für einen Körper im thermischen Gleichgewicht $a = \epsilon$. Somit haben wir die Reflektivität auf die für uns relevanteste Größe zurückgeführt. Wir erhalten $r_O = 1-\epsilon_O$ und nach dem Einsetzen in die obige Gleichung schließlich:
\[ P_\text{Reflektiert} = (1-\epsilon_O) \, \tau_L \, P(T_U) \]
Um dies nochmal hervorzuheben – die Umgebung wird also durch nur einen Parameter beschrieben – ihre Temperatur $T_U$. Das lässt sich entweder grob abschätzen, wird aber in der Praxis aber oft auch so gehandhabt, dass man $P(T_U)$ mit der Infrarotkamera direkt misst (wobei ich hier nun nicht im Detail darauf eingehe).
Von dazwischenliegender Luft emittierte Strahlungsleistung
Somit bleibt als letzte Größe der Einfluss der Luft zu bestimmen. Wir finden ein bekanntes Vorgehen wieder – auch hier nehmen wir an, dass sich die Luft wie ein grauer Körper verhält. Somit ist
\[ P_\text{Luft} = \epsilon_L P(T_L) \]
Wie zuvor formen wir zunächst um. Für Luft nehmen wir an, dass diese die Strahlung nicht reflektiert, also $r_L$ = 0. Durch einsetzen in Gleichung (1) und umformen erhalten wir abschließend noch $\epsilon_L = 1-\tau_L$ und einsetzen führt auf
\[ P_\text{Luft} = (1-\tau_L) P(T_L) \]
Wenn wir nun all diese hergeleiteten Terme in Gleichung (3) einsetzen sind wir bei der Messgleichung angekommen.
Die Messgleichung
\[ P_\text{Gesamt} = \tau_L \, \epsilon_O P(T_O) + (1-\epsilon_O) \, \tau_L \, P(T_U) + (1-\tau_L) P(T_L) \]
Damit gibt es 4 Parameter die ermittelt und eingestellt werden müssen um die Voraussetzung für eine akkurate Temperaturmessung zu schaffen.
- Die Emissivität der Oberfläche des Versuchsobjektes $\epsilon_O$
- Eine der Umgebung zugeordnete Temperatur $T_U$ (auch „reflektierte scheinbare Temperatur“)
- Die Temperatur der Atmosphäre zwischen Kamera und Objektiv $T_L$
- Der Transmissionskoeffizient der Atmosphäre zwischen Kamera und Objektiv $\tau_L$
Der Koeffizient $\tau_L$ kann von den meisten Softwaretools mit denen thermografische Daten ausgewertet werden automatisiert aus der Distanz zwischen Infrarotkameraobjektiv und Versuchsobjekt, sowie aus der relativen Luftfeuchtigkeit abgeschätzt werden.
Natürlich hängt es auch von der jeweiligen Situation ab, welche Faktoren nun einen großen Einfluss haben. Betrachtet man ein im Infrarotbereich hochreflektierendes Material (also $\epsilon_L$ sehr klein) wie Aluminium, dann ist eine gute Abschätzung von $T_U$ unerlässlich – denn diese wird einen nicht zu vernachlässigenden Anteil an der Gesamtstrahlung haben. Ist der Abstand zwischen Objektiv und Versuchsobjekt sehr klein, dann spielt die Luft dazwischen nur eine untergeordnete Rolle.
Man sieht also – während zwar das kontaktfreie Messen mit Infrarotkameras jeder Preisklasse als simples „Point and Click“ verkauft wird, gibt es viele Faktoren die bei nicht sachgerechter Handhabung und Bedienung die ermittelten Werde mehr als fragwürdig machen. Korrekt durchgeführte thermografische Messungen hingegen liefern verlässliche Werte – es gibt nur, wie man sieht, einiges zu berücksichtigen.
Auch darüber hinaus kann weiteres Finetuning nötig sein. Die Kamera selbst emittiert (auch in ihrem Inneren) elektromagnetische Strahlung im langwelligen Bereich des Spektrums die auf dem Sensor auftrifft und das Ergebnis beeinflusst. Daher können manche Infrarotkameras gekühlt werden um diese Eigenstrahlung so weit wie möglich zu reduzieren. Die Transmissivität des Infrarotkameraobjektives hat ebenfalls noch Einfluss wieviel von $P_\text{Gesamt}$ tatsächlich ein Signal am Sensor verursacht. Die Softwaretools zur Auswertung bieten normalerweise eine entsprechende Einstellmöglichkeit um die Transmissivität der Objektive festzulegen um dies korrekt mit einbeziehen zu können. Man sieht – um so weiter ins Detail man geht um so mehr Faktoren spielen eine mehr oder weniger große Rolle. Durch sauberes und systematisches Messen lassen sich dennoch reproduzierbare und gute Ergebnisse erzielen.
