Teil 3 – Emissionskoeffizient
In diesem Teil der „Wie funktioniert eine Infrarotkamera?“ Serie beschäftigen wir uns erstmalig damit, welche Dinge man berücksichtigen muss wenn man Temperaturen mit einer Infrarotkamera messen will. Die wirkliche Welt ist nicht ideal, aber nach den letzten beiden Artikeln haben wir das nötige Rüstzeug um uns einen weiteren Schritt vorzuwagen. Heute werden wir sehen, dass das Planck’sche Strahlungsgesetz zwar sehr hilfreich ist, wir aber der Kamera noch mindestens eine weitere Information geben müssen, damit sie die Temperatur bestimmen kann.
Was zuletzt geschah
Im letzten Eintrag haben wir uns angesehen was das Prinzip hinter der Temperaturbestimmung ist. Dabei haben wir festgestellt, dass die Helligkeit die die Kamera wahrnimmt direkt mit der Temperatur eines Körpers zusammenhängt. Genauer gesagt über die Fläche unter der Kurve welche durch das Planck’sche Strahlungsgesetz gegeben ist und zwar in dem Wellenlängenbereich in welchem die Kamera sensibel ist.
Inhalt der Artikelserie
Teil 1 – Grundlegendes
Teil 2 – Temperaturbestimmung
Teil 3 – Emissionskoeffizient
Teil 4 – Die Messgleichung
Schwarze Körper
Mit dem Planck’schen Strahlungsgesetz haben wir bisher viel erklärt. Aber es beschreibt einen Idealfall – und zwar den eines sogenannten schwarzen Körpers. Der Name kommt nicht von ungefähr, kann aber mitunter etwas verwirrend sein. Ein Schwarzer Körper absorbiert jede Strahlung die auf ihn eintrifft, egal welche Wellenlänge sie hat. Wenn das jetzt alles wäre was er macht, wäre er tatsächlich schwarz. Was ihn aber noch zusätzlich auszeichnet ist der Umstand, dass er auch wieder Strahlung abgibt. Dieses charakteristische Spektrum hängt nun aber eben nur von seiner Temperatur ab!
Eine weitere Eigenschaft können wir aus dem Kirchhoffschen Strahlungsgesetz schließen. Es besagt, dass ein Schwarzkörper im thermischen Gleichgewicht (wenn sich die Temperatur eines Körpers also nicht ändert) genau so gut Strahlung absorbieren kann, wie er sie emittieren kann. Kein anderer Körper der nur aufgrund seiner eigenen Temperatur strahlt kann also mehr Strahlung abgeben!
Aber warum ist das so? Nun, wir haben ja den Schwarzen Körper als etwas kennengelernt das alle Strahlung die auf ihn eintrifft absorbiert. Komplett. Jetzt hat uns das Kirchhoffsche Strahlungsgesetz gesagt, dass der schwarze Körper genauso gut emittiert wie er absorbiert. Nachdem er maximal absorbiert folgt, das er auch maximal emittiert. Das ist gut zu wissen und liefert uns quasi eine Referenz dafür, was höchstens möglich ist! Und das ist ja genau durch das Planck’sche Strahlungsgesetz beschrieben.
[expand title=“Planck’sches Strahlungsgesetz zur Erinnerung (ausklappbar)“]
\[w(\lambda,T) = \frac{2hc^2}{\lambda^5}\left(\exp{\left(\frac{hc}{\lambda k_B T}\right)}-1\right)^{-1} \]
Hier steht $c$ für die Lichtgeschwindigkeit, $h$ das Planck’sche Wirkungsquantum, $\lambda$ die Wellenlänge, $k_B$ die Boltzmann Konstante und $T$ für die absolute Temperatur des Körpers.
[/expand]
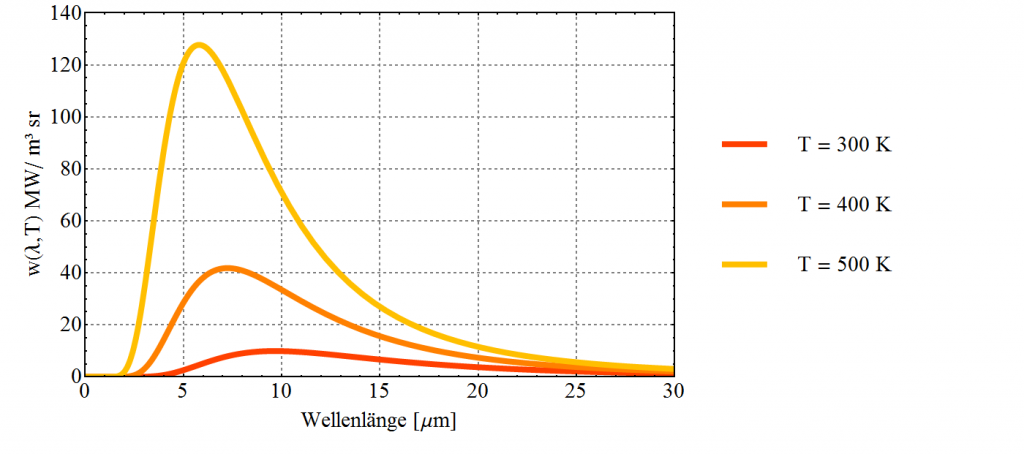
Tatsächlich kann man sich „relativ“ einfach etwas bauen, was in etwa einem idealen Schwarzkörper ähnelt, zum Beispiel einen hohlen Quader. Malt man diesen innen nun schwarz an und bohrt ein kleines Loch in eine Wand dann wird etwas Licht hineinkommen. Dieses wird an den Wänden innen dann immer wieder reflektiert und immer weiter abgeschwächt – nur sehr wenig wird wieder durch die kleine Bohrung nach draußen gelangen. Beobachtet man dann die elektromagnetische Strahlung welche die Öffnung verlässt mit einem Spektrometer, würde man erwarten, dass sie den Spektren in Abbildung 1 ähnelt. Nicht perfekt weil es ja kein idealer Schwarzkörper ist, aber doch ähnlich. Aus diesem Grund ist die Schwarzkörperstrahlung auch unter dem Namen Hohlraumstrahlung bekannt.
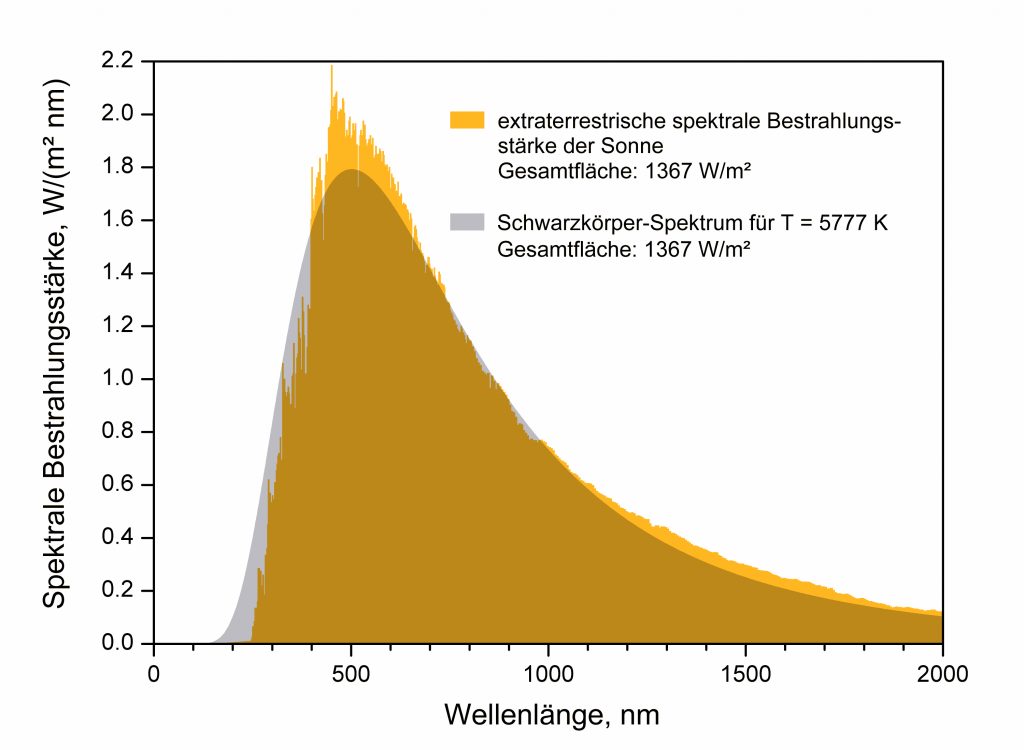
Es gibt übrigens einen sehr prominenten, beinahe idealen Schwarzkörper den jeder schon gesehen hat und regelmäßig sieht – die Sonne. In Abbildung 3 ist ein Vergleich der beiden Spektren gezeigt.
Graue Körper und der Emissionsgrad
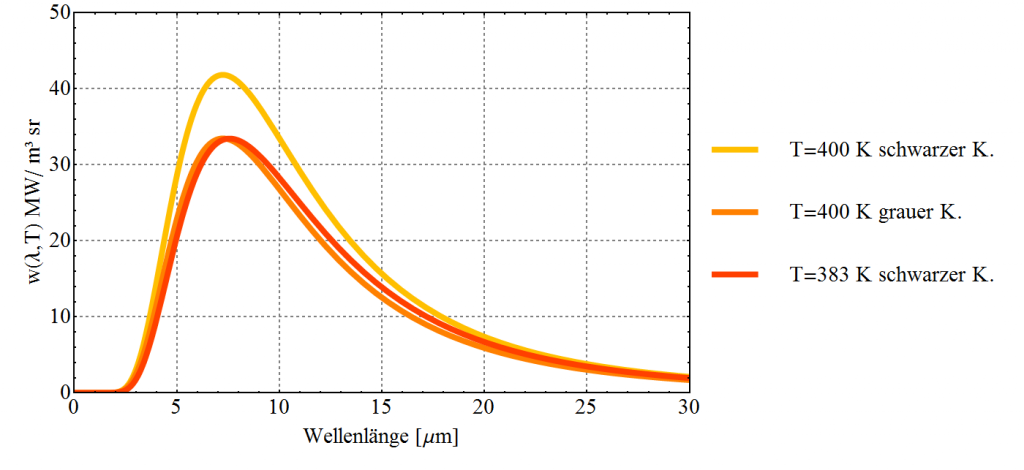
Es gibt einige Dinge in der Welt die sich ähnlich verhalten wie ein schwarzer Körper aber nicht ganz so viel Strahlung abgeben. Solche Objekte nennt man graue Körper. Sie kennzeichnen sich dadurch, dass sie um einen fixen Faktor weniger Strahlung abgeben als ein Schwarzkörper. Der Faktor heißt Emissivität und wird meistens mit $\epsilon$ angegeben. Sie liegt für graue Körper zwischen 0 und unter 1. Kleiner als 1 deswegen, weil $\epsilon=1$ genau dem Schwarzkörper entspräche. In der nächsten Abbildung sind die Spektren eines schwarzen und eines grauen Körpers mit $T=400\;\text{K}$ gegenübergestellt.
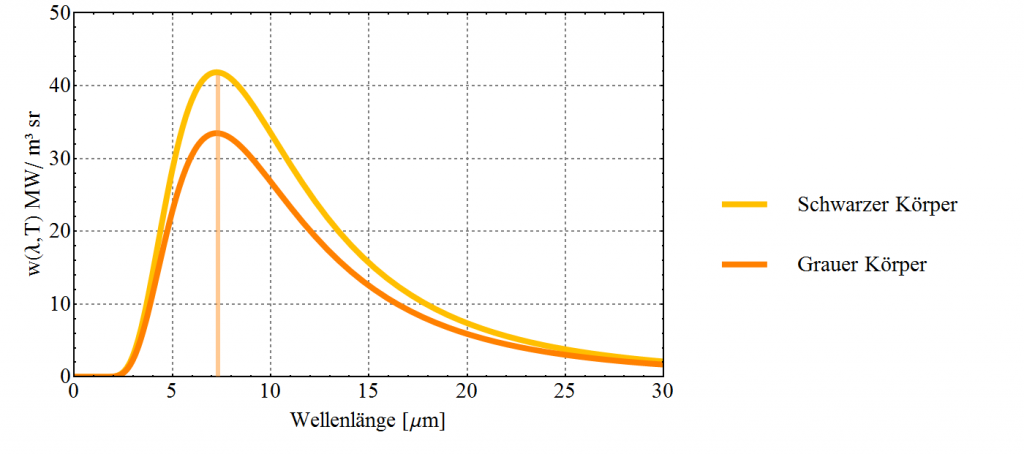
Eine interessante Beobachtung kann man hierbei machen – die maximale Abstrahlung liegt bei der gleichen Wellenlänge, also bei ca. $7.2\;\mu\text{m}$. Man könnte nun vielleicht vermuten, dass ein schwarzer Körper der etwas kühler ist, also so um die $383\;\text{K}$ das gleiche Spektrum ergäbe wie der graue Körper. Aber Achtung – wir hatten im ersten und zweiten Teil dieses Artikels bereits etwas festgestellt – das Maximum der Strahlungsabgabe wandert mit höherer Temperatur immer weiter nach links bzw. mit niedrigerer immer weiter nach rechts. Der kühlere schwarze Körper gibt also bei einer etwas größeren Wellenlänge, konkret sind es $7.5\;\mu\text{m}$, das Maximum an Strahlung ab. Aber auch sonst stellt man, wie in der nächsten Abbildung ersichtlich, doch recht deutliche Abweichungen fest.
Der Emissionskoeffizient kann bei Infrarotkameras eingestellt werden und ist eine für sie wichtige Information um Temperaturen richtig zu messen. Dabei modifiziert die Kamera allerdings nicht die interne gespeicherte Tabelle mit der sie ankommender Strahlung eine Temperatur zuordnen kann. Tatsächlich berechnet sie nämlich – bevor sie in der Tabelle nachschlägt – aus dem Signal am Sensor wieviel Strahlung bei ihr angekommen ist. Diese Berechnung erfolgt nach der sogenannten Messgleichung welche wir in einem der Folgeartikel noch kennenlernen werden.
Als Abschluss möchte ich noch anmerken, dass auch graue Körper eine Idealisierung sind. Reale Körper emittieren zwar thermisch nie mehr als durch das Planck’sche Strahlungsgesetz gegeben, aber sie strahlen auch nicht zwangsläufig über alle Wellenlängen um einen fixen Faktor weniger ab. Die Emissivität kann von weiteren Größen abhängen wie zum Beispiel der Temperatur des Körpers, der Wellenlänge, und sogar der Richtigung in die abgestrahlt wird!
Aber glücklicherweise kann man in bestimmten Bereichen die meisten realen Körper ganz gut als graue Körper beschreiben. Und da wir in der Thermografie auch nur in bestimmten Wellenlängenbereichen messen, ein typischer Bereich den wir schon kennengelernt haben ist der von $8-12\;\mu\text{m}$, stellt der Emissionskoeffizient hier eine wichtige Größe dar.
Die Essenz ist: Auch wenn die wirkliche Welt uns allerlei Komplikationen um die Ohren wirft, es gibt Möglichkeiten diese in den Griff zu bekommen.

2 Kommentare