Movie physics taken seriously
Usually movies are critisised for the way they treat physics. Specifically because of the liberties they take or how they outright ignore laws of nature. I want to approach this from a different angle. In this series we take what happens in movies serious and look at the consequences that has if the usual laws of nature apply.
With this premise this article is in contrast to this one. The author explains why Luke Skywalker will die even though Han Solo stuffs Luke into the Tauntaun. However, it uses some faulty assumptions – the mass of the tauntaun is completly neglected for instance. Another article simplifies too much and estimates how long it takes until the Tauntaun is frozen. Even the Mythbusters have tackled this problem, however they work with higher temperatures and without wind.
We will try to answer the following question:
Which properties must the Tauntaun have for Luke to survive until Han has managed to build a shelter?
Notice: This is an abbreviated and translated version of my original article. It goes into a little bit more detail about why certain things can be neglected and has an additional section that tests the proposed model with an experiment.
What happens in the movie
For everyone who doesn’t know the scene I’m talking about – here’s a short summary. A wounded Luke is lost on the ice planet Hoth. The night is closing in and the temperature drops fast. Leia, Han, C3PO and R2D2 are getting nervous because the protagonist hasn’t returned until eventually Han decides to go looking for him. He finally manages to find him, however at this point Luke is quite exhausted. Even Han’s Tauntaun perishes due to circumstances unbeknownst to us. This makes a return to base impossible. Han cuts open the Tauntauns belly and stuffs Luke in there to save him from certain death while he begins building ashelter. While we don’t get to see the stuffing in part in the movie it certainly is mentioned in the script!
The neccessary physics
The following two expandable boxes explain some of the basic physics. Some concepts such as heat capacity are introduced and explained.
[expand title=“Some physics – Heat and temperature“]
Physics – Heat and Temperature
What does it actually mean when a body has a certain temperature $T$? From a physicists point of view the relevant quantity is the internal energy $Q$. In this context the terms heat or heat energy are used interchangeably.
Therefore, objects can be heated by increasing their internal energy. To heat a liter of water (=$1$ kg) one might, for instance, use a water boiler. But how much energy actually is needed to heat one kilogramm of water by one Kelvin ($=1o^\text{C}$) is given by another quantity. It is the specific heat capacity $c_V$. It tells us, that we need to supply $4 182$ Joule to heat our liter of water from $20\;^o\text{C}$ to $21\;^o\text{C}$. This is approximately the energy that you’ll have to supply if you want to carry a $100$ kg package from the ground floor to the first floor (assuming a floor is $4.3$ m high). That’s actually quite something!
What is important here is that we have a method to calculate how much energy we need to increase the temperature of an object or body by a certain amount!
[/expand]
[expand title=“Example – Heat and temperature“]
Example – Heat and Temperature
We want to heat $1$ kg water from $20$ °C to $100$ °C. To do this we use a water boiler with a power of $P = 2500$ W. How long does it take until we can enjoy our cup of tea?
First – let’s think about what it actually means that something has a power of $2500$ W. The W is an abbreviation for Watt and this is actually an abbreviation for energy (Joule) per second (J/s). So with the water boiler from above we can heat a liter of water in about $1.7$ s by 1°C.
However, we are interested in a temperature increase of $\Delta T=80$ °C! We already know the specific heat capacity. For $20$ °C warm water it is $c_V = 4182 J/kgK$. Now let’s assume that it will not change much during the heating process. That is a simplification, but as long as the boiling point is not reached it is justified.
The heat energy that we have to supply in total is
\[ \Delta Q = c_V \cdot m\cdot \Delta T \]
Since $m=1$ kg it follows that $\Delta Q = 334560$ J. Now there’s just one last step left. We know the energy that we need to supply and we know the rate at which our water boiler can to exactly that. That means that all that’s left to do is a simple division:
\[ t = \frac{\Delta Q}{P} = 134\; \text{s} \approx 2.2\; \text{minutes}\]
[/expand]
Things we know and assumptions we make
General Assumptions
We have to make some very basic assumptions here. For instance we assume that Luke and Han are humans or at least life forms that are, in the properties relevant to our calculation, pretty similar to humans. Therefore we know the core body temperatures of these characters. In Luke’s case we assume it to be $37$ °C. That means for the time being he’s not undercooled yet. Just exhausted.
Planet Hoth
What do we know about the environmental conditions? At night the average temperature on hoths equator is approximately $T_A =-60\;^o\text{C}$.
The wind speed is also an important factor for the cooling process. We could try to estimate it from watching the movie or we could use a value from a comparable ice desert. This site lets us know that the average windspeed in antarctica is about $37\;\text{km/h}$. For my taste the movie wind looks faster than that so let’s double it and use $74\;\text{km/h}$ which corresponds to $v_W\approx 20\;\text{m/s}$. By the way our estimate is still below the maximal wind speed measured during gusts. That would be $248.4\;\text{km/h}$.
Luke
Now we think about Luke for a while. First we have to know how much heat a human can store per mass and temperature. We’re looking for the average specific heat capacity of a human. Luckily there are some studies (Takata 1977, Giering 1995) adressing this question. If the ratio $W$ of water mass to body mass is known the specific heat capacity of a human is given by
\[ c(W) = 4190(0.37+0.63W)\]
Ok so now we have found an answer but got a different question. How do we estimate $W$?
I found another paper (Watson 1980) that tells us how to arrive at an value for $W_\text{luke}$. It gives a function that calculates that value from a persons age $a$ in years, size $h$ in meters and mass $m$ in kg. What they did to arrive at that was measuring these properties for a lot of men and women. After that for each gender they chose a mathematical function that reproduced these values best with the parameters given.
[expand title=“The water-ratio function“]
\[ W_\text{Luke}(a,h,m) = \frac{1}{m} \left( 2.447 – 0.09516a + 10.74h + 0.336m \right) \]
[/expand]
But where do we get Lukes data from? Again, there’s a pretty extensive encyclopedia out there. So $m=77\;\text{kg}$, $h=1.72\;m$ and Luke’s age in years at the time he was stationed at Hoth is $a\approx 22\;\text{y}$. To convert between star-wars years and our years it helps to take a quick look at the appropriate calendar system. We arrive at
\[ W_\text{Luke} =0.58 \]
\[ c_\text{Luke} = 3083 \;\text{J/kgK} \]
So far so good. As mentioned before the value of $c_\text{Luke}$ is an average. Organs, bones, body fluids and other things that are inside a humang body all have different heat capacities.
If we assume that Luke does not already suffer from hypothermia when Han finds him, we can estimate his core body temperature with $37\;^o \text{C}$. For mild hypothermia it would be $35\;^o\text{C}$ and for severe $28\;^o\text{C}$. If Luke’s core body temperature drops below that we assume that he will die.
The Tauntaun
We continue with the Tauntaun and start with the following simplification. We assume that it has similar thermophysical properties (e.g. it’s heat capacity) as Luke. That’s actually not that big of a stretch as long as it’s body has a similar water-ratio.
We’ll also assume that it has a thick insulating layer of thickness $d$. In the movie we can clearly see that there’s a layer of fur. However more importantly there probably is a layer of fat below that. Fat has a heat conductivity of $\lambda=0.38\;\text{W/mK}$. The smaller that value the better the thermal insulation – and fat is a pretty good thermal insulator.
Below that then are the muscles and entrails of the Tauntaun. Oh and also Luke Skywalker. All the heat that’s stored in these things has to leave through the insulating layer.
Now we need to know the Tauntaun’s weight. From the movie it looks – when compared to Han – as if the Tauntaun’s were comparable to a horses when it comes to size. The average mass of a large riding horse is approximately $550$ kg. So we’ll choose that as $m_\text{Tauntaun}=550\;\text{kg}$. However, some people use masses of up to $1300\;\text{kg}$. With our value we may neglect the weight of its tail. Nonetheless its influence on the cooling process is probably small.
Later it will be relevant how large the surface of the Tauntaun is. To this end we imagine it as a half-cylinder lying on the ground (Turnpenny 2000). The cylinders radius is $0.7\;\text{m}$ and its length $1.5\;\text{m}$. This yields a surface of $A=4.8\;\text{m}^2$.
The Shelter
There is a rather big debate what the type of shelter Han errected. Some think it’s a tent that he brought from aboard the Millenium Falcon. Others say that he just built an igloo but with futuristic tools. A tent (especially in the Star Wars universe) might be errected in a couple of minutes. But what about an igloo? How long would that take?
since I’m not an expert on that lets use values from people that are. On this page it is said that it can take between 3 and 6 hours to build an igloo. If we assume that Han has some advanced tools at his disposal he might be able to shorten the time to 1 to 2 hours. That is how long Luke has to stay alive.
Now we have collected all the data we need.
Physics – How things cool
Newton’s law of cooling
It is usually Newton’s law of cooling that is brought up to solve this problem. It tells us that a body’s rate of cooling depends directly on the temperature difference between the body and its environment. For our case this would initially be $97\;\text{K}$. A closer look at this law can be found in the following expandable box.
[expand title=“Newton’s law of cooling“]
\[ \frac{c m}{A} \frac{dT}{dt} = U (T(t)-TA )\]
The rate of cooling is given by the derivative $dT/dt$. It tells us how many Kelvins per second the Luketauntaun cools at any given moment. The factor $U$ is called the thermal transmittance. It basically tells us how much heat is lost per second, area and kelvin. It’s easy to imagine that something that shares a bigger surface with its environment will lose more heat than something with less surface. The same goes for the temperature – the higher it is as compared to the environment the higher the heat loss.
We also notice that the temperature changes slower the higher the heat capacity of the system. It is given by the product of $c\;m$. An example would be a styrofoam box filled with cold beverages. The more beverages you put in the longer they are going to stay cool.
[/expand]
Now someone could say: „But what about heat loss due to thermal radiation?“. And that would be a valid objection! This heat exchange mechanism is not considered by Newton’s law of cooling. However, if we look into it we realise that due to the strong winds on Hoth heat transfer by convection is the dominant mechanism. In the temperature range we are interested in it is about 10 times as large as radiative cooling. It’s therefore safe to neglect it and stick with the much easier to handle Newtonian law of cooling.
The temperature function
All that’s left to do is solve the differential equation above. The result is:
\[T(t) = (T_0 – T_A) e^{-\frac{U A}{C} t} + T_A\]
Most of these quantities we already know: $C=c (m_\text{Luke}+m_\text{Tauntaun})$ is the Luketauntaun’s heat capacity, $A$ the surface shared with the environment, and $U$ the thermal transmittance of the system. It depends on the thickness of the insulating (fat) layer, it’s heat conductivity $\lambda$ and on the heat transfer coefficient on the inner and outer surface of the layer of fat. The expandable box below gives a more detailed look and explanation of the associated equation.
[expand title = „The thermal transmittance of the Luketauntaun“]
The thermal transmittance tells us how much heat is exchanged with the environment per second, area and Kelvin. The larger the surface area of a body in contact with its environment the more heat can be transported through it.
\[U=\frac{1}{\frac{1}{\alpha_\text{Air}} + \frac{d}{\lambda} + \frac{1}{\alpha_\text{Water}} }\]
Of course there are more quantities influencing this. The heat transfer coefficients on the inner and outer side of the fat layer. Their values are larger the better the heat transfer. For instance, water is much more efficient than air. In our case we have strong winds on the outside and therefore $\alpha_\text{Air}=3+3v_W\;\text{W/m}^2\text{K}$, and a mixture of blood and bodily fluids (approximating water) on the inside. Therefore $\alpha_\text{Water}\approx 500\;\text{W/m}^2\text{K}$.
The composition of the insulating layer is also considered in this. It’s clear that the thickness $d$ factors in – a paperthin layer of styrofoam will do almost nothing, while a $10\;\text{cm}$ thick will provide really good thermal insulation. Then there’s the type of insulator used. Styrofoam and fat are good, but, for instance, copper conducts heat very well. This is summed up in the thermal conductivity $\lambda$.
[/expand]
Results
Now we vary some parameters and see where that takes us. We distinguish two cases – the worst case and the best case.
The worst case
In this scenario we choose some parameters in a way that is detrimental to Luke’s survival. To this end we assume that the Tauntaun has cooled off a bit since it perished, and that Luke himself already suffers from mild hypothermia. We start with $T_0=35\;^o\text{C}$. We also increase the windspeed by $1/3$rd, yielding $v_W=40\;\text{m/s}$. Additionally, to make matters even worse, we assume that Han needs two hours to construct a shelter. Maybe even the ambient temperature is a little lower, so let’s set $T_A=-80\;^o\text{C}$. It is also possible that we overestimated the Tauntaun’s mass, maybe a large riding horse wasn’t a good comparison at all! So let’s reduce that too and use $m_\text{Tauntaun}=450\;\text{kg}$.
Now we calculate the temperature course for different thicknesses of the insulating fat layer.
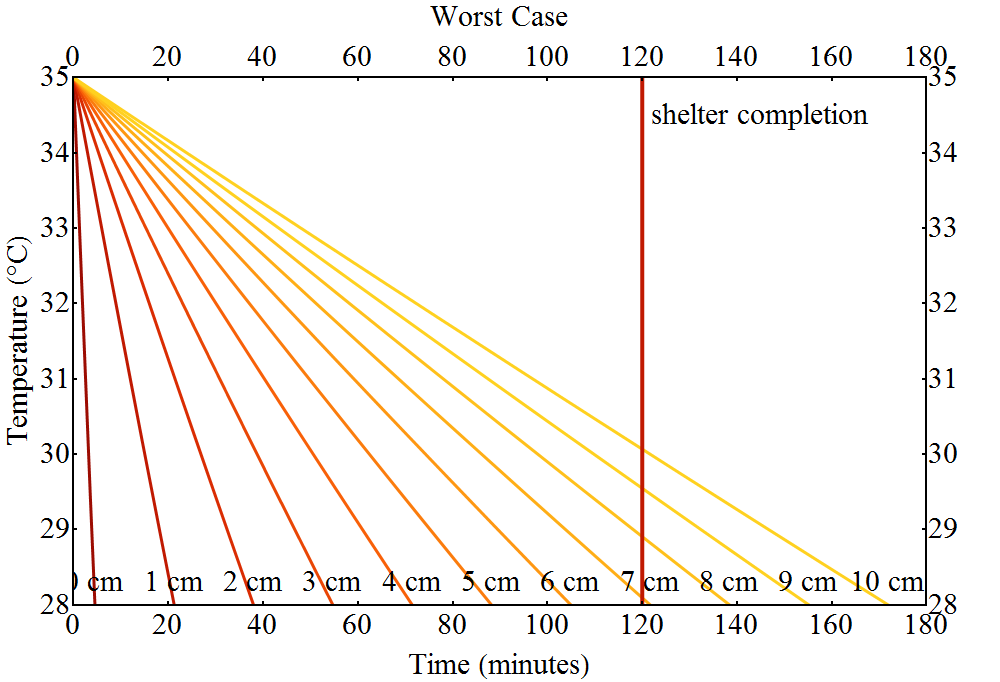
The figure above shows some curves, all annotated with the corresponding thickness of the insulating fat layer. The colouring indicates how good the result is for Luke – the more yellow the better. The longer his body temperature stays above $28\;^o\text{C}$ the better his chances of survival.
For the worst case scenario we can note the following:
If the Tauntaun’s fat layer is at least $7\;\text{cm}$ thick Luke does not suffer severe hypothermia while Han builds the shelter. However, he’s almost there and a little bit of safety margin would be a good idea. With a fat layer of $8\;\text{cm}$ Luke would still have a body temperature of $29\;^o\text{C}$ – low but with already increased chances of survival.
So $8\;\text{cm}$ is our fat layer thickness result here. This gives Luke an actual chance to survive the night.
The best case
As in the worst case scenario we vary some parameters differently. This time, however, we adjust them in such a way that it is easier for Luke to survive. That means that we set $T_A=-60\;^o\text{C}$, $T_0=37\;^o\text{C}$, $v_W=20\;\text{m/s}$, $m_\text{Tauntaun}=550\;\text{kg}$ and we give Han a speed boost, allowing him to build an igloo in only $60\;\text{min}$.
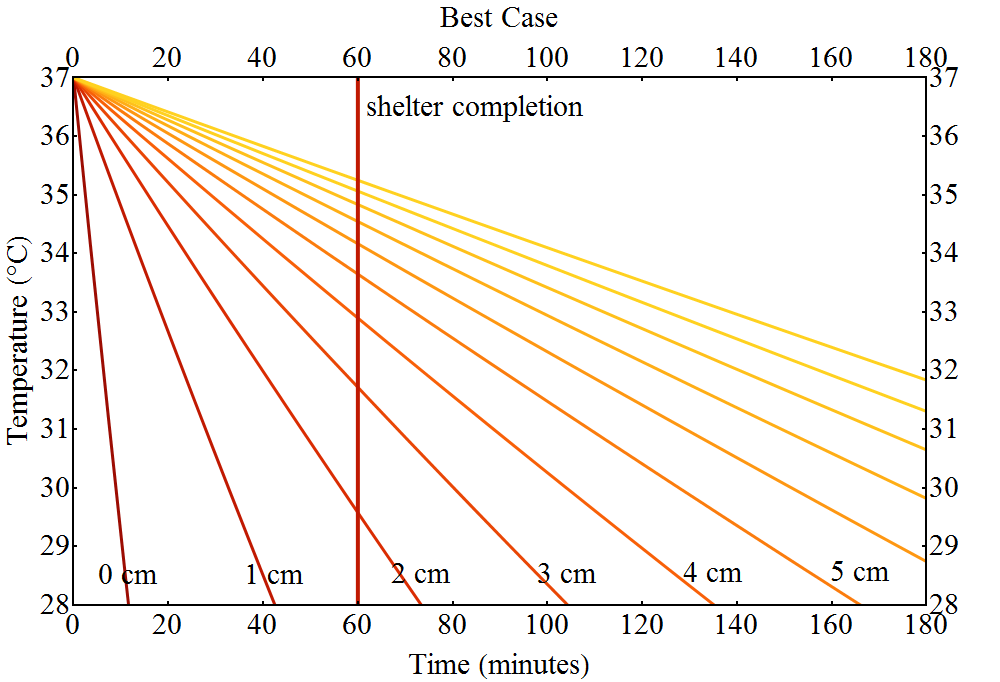
These choices increase Luke’s chances to survice the night quite a bit. Now the Tauntaun is only required to have a layer of fat that is $2\;\text{cm}$ thick.
Conclusion
After all the work we did we can now say that Luke’s survival is likely if the Tauntaun’s thermally insulating fat layer has at least a thickness between $2\;\text{cm}$ and $8\;\text{cm}$.
If you finally get to a result it is useful to think about wheter it is a realistic one or not. In our case we can take a look at terrestrial life forms that live (like Tauntauns) in a natural environment that resembles Hoth. A polar bear would be a good candidate for that. And we find that they can have fat layers of up to $8.6\;\text{cm}$!
Another reason for Luke’s survival is the large mass of the Tauntaun. It is at least 6 times that of Luke’s and consists mainly of materials (tissue and water) that stores heat well. Getting rid of all that heat just takes its time!
Of course we made some simplifications that are questionable. The cut at the Tauntaun’s belly for instance – we can expect an additional heat loss there. But on the other hand we can argue that Han closed it off as well as possible or that Luke’s body produces some heat on its own.
All in all I’d say that Luke has some actual chance of surviving without suffering from severe hypothermia. However, problems that arise from lying around in the intestines of another life-form (oxygen supply for Luke, risk of infections due to open wounds, …) are something I excluded from this analysis.
By the way our results are even consistent with the Mythbusters Episode. If we choose the parameters as shown in that episode the fat layer that yields the same results (Luke having a temperature of $33^o\;\text{C}$ after $2.5\;\text{h}$) would be $2\;\text{cm}$ thick.
So all in all it is entirely possible that Luke survives the night. Assuming that he does, does not even lead to absurd properties of the Tauntaun (like a $10\;\text{m}$ thick fat layer for instance). And we even find similiar fat layer thicknesses in polar bears.
Literature
J.R. Turnpenny et. al., 2000, Thermal balance of livestock: 1. A parsimonious model. Agricultural and Forest Meteorology, Vol. 101, 1, pp15–27
K. Giering, 1995, Determination of the specific heat capacity of healthy and tumorous human tissue, Thermochimica Acta, Vol. 251, pp199-205.
A.N. Takata et. al., 1977, Laser-induced thermal damage of skin, USAF school of aerospace medicine.
P.E. Watson et. al., 1980, Total body water volumes for adult males and females estimated from simple anthropometric measurements, The American Journal of Clinical Nutrition, Vol. 33, pp27-39.
C.T. O’Sullivan, 1990, Netwon’s law of cooling – A critical assessment, American Journal of Physics, Vol. 10, pp956-960
