Die Raumzeit mit Magnetismus krümmen? Wie soll das denn gehen? Eine Frage die sich vielleicht einige stellen. Meistens ist zwar geläufig, dass Massen laut allgemeiner Relativitätstheorie die Raumzeit verzerren, aber, dass dies auch mit elektrischen oder magnetischen Feldern möglich ist, ist nicht so bekannt. Grund für diesen kurzen Artikel ist ein gerade erschienenes Paper, das sich genau mit diesem Thema beschäftigt. Ja, die künstliche Krümmung der Raumzeit finde ich durchaus spannend. Anschaulich kann man sich das ausgehend von Einsteins wohl bekanntester Gleichung vorstellen.

Energie

\[ E=mc^2 \]

Diese Gleichung beschreibt die Ruheenergie eines massebehafteten Teilchens. Besonders spannend ist hierbei das Gleichheitszeichen – man kann das ganze in beide Richtungen lesen! So kann man diese Gleichung ja auch so interpretieren, dass jeder Energie eine Masse zugeordnet werden kann. Klar, diese ist (weil $c^2$ so groß ist) um 16 Größenordnungen kleiner als die Energie, aber dennoch wäre

\[ m = \frac{E}{c^2} \]

mit $c\approx 3\cdot 10^8\;\text{m/s}$.

So weit so gut. Man kann also einem ruhenden Teilchen eine gewisse Ruheenergie zuordnen. Wenn es sich gleichförmig bewegt kommt noch die kinetische Energie obendrauf. Heißt das im Umkehrschluss, dass bewegte Teilchen also etwas schwerer sind als ruhende? Tatsächlich kann man das so interpretieren. Energie kann man aber nicht nur Teilchen zuordnen, möglich ist das auch für …

Elektromagnetische Felder

Dazu holen wir ein kleines bisschen aus. Tatsächlich sind magnetische und elektrische Felder zwei Seiten derselben Medaille – das eine kommt, sofern man sich nicht nur im statischen Bereich bewegt, ohne das andere nicht vor. James Clerk Maxwell hat, in den von ihm entwickelten und später nach ihm benannten Maxwellgleichungen, diese beiden, ursprünglich voneinander unabhängigen Gebiete, miteinander vereint.

Experimentell gab ein Zufall während einer Vorlesung von Hans Christian Oersted dabei die Richtung vor. So beobachtete er 1820, dass ein stromdurchflossener Draht dazu führt, dass die Nadel eines in der Nähe des Drahtes liegenden Kompasses abgelenkt wird. Die durch den Draht fließenden Elektronen sind ein elektrischer Strom, und diese bewegten Ladungen führen zu einem Magnetfeld das den Leiter einhüllt. Elektrische Felder die sich zeitlich ändern und elektrische Ströme erzeugen also magnetische Felder und umgekehrt.

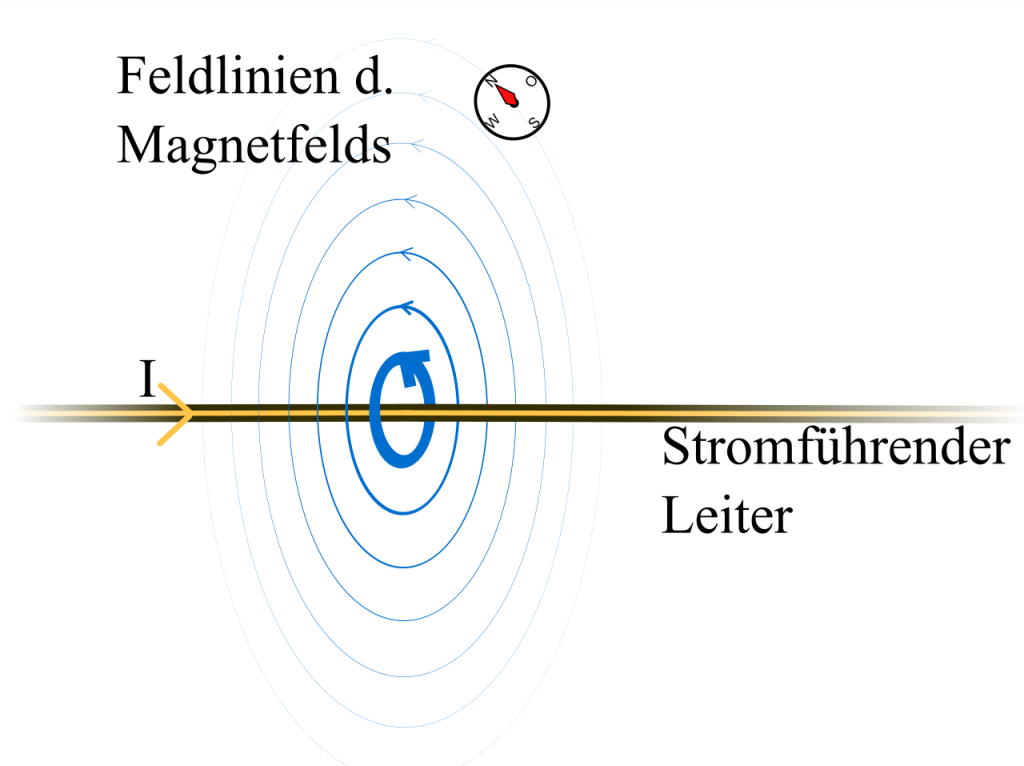
Elektromagnetismus – Elektrizität und Magnetismus – ist die Folge einer grundlegenderen physikalischen Wechselwirkung: der elektromagnetischen Wechselwirkung.

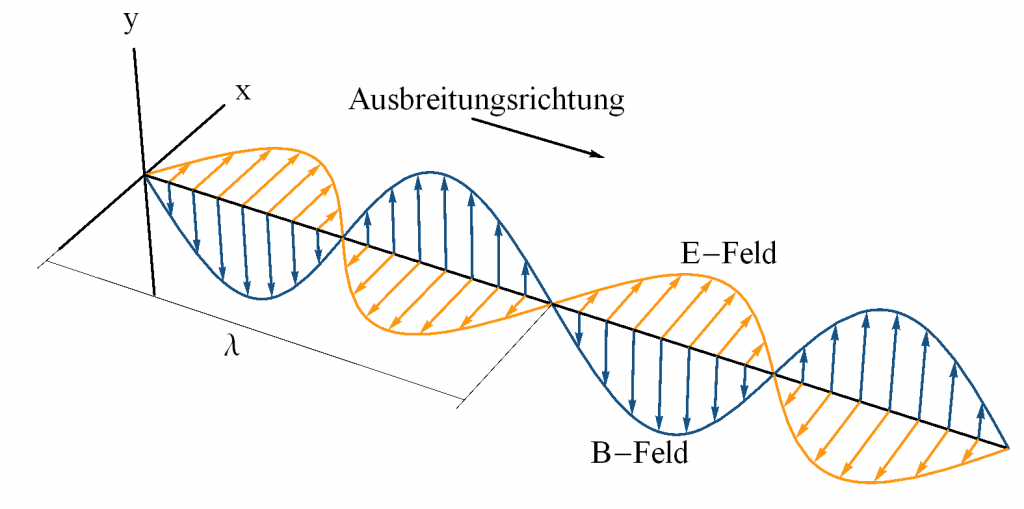
Diese Wechselwirkung wird mit Feldern beschrieben. Licht zum Beispiel eine elektromagnetische Welle welche aus einem rechtwinklig zur Ausbreitungsrichtung stehenden elektrischen Feld, und einem rechtwinklig dazu stehendem magnetischen Feld besteht. Und solchen Feldern kann nun ebenfalls Energie zugeschrieben werden. Das spürt man auch wenn man sich einfach ins Licht der Sonne begibt – dieses Licht, welches ja aus elektromagnetischen Wellen besteht, erwärmt einen. Verbringt man zu viel Zeit beim Sonnenbaden riskiert man sogar einen Sonnenbrand – die Haut verbrennt weil ihr zuviel Energie zugeführt wird.

Und hier sind wir nun am Ende dieses vereinfachten Arguments. Wenn elektromagnetische Feldern eine gewisse Energie zukommt, dann kann man mit $E=mc^2$ die Brücke dazu schlagen, dass dieser Energie eine gewisse Masse entspricht. Und Massen krümmen die Raumzeit. Das ist natürlich eine sehr starke Vereinfachung, aber ein unserer Welt zugrunde liegendes Prinzip tritt zutage – auch Felder sind Energieträger und beeinflussen die Raumzeit.

Dieser Umstand, dass auch Felder Träger von Energie sein können, spielt auch für Atome eine Rolle. Misst man nämlich genau nach stellt man fest, dass Atome schwerer sind als die Summe der Massen ihrer Bestandteile. Dafür verantwortlich ist die Energie der nuklearen Bindung, die starke Kernkraft die die Kernbestandteile zusammenhält, das Phänomen ist als Massendefekt bekannt.

Raumzeit?

Es schreibt sich leicht – die Raumzeit wird gekrümmt. Kann man sich das noch vorstellen? Zumeist wird das Bild einer aufgespannten Gummiplane bemüht auf welche eine schwere Kugel gelegt wird. Eine Vertiefung bildet sich  durch das Gewicht der Kugel, die Gummiplane ist hier die Analogie zum gekrümmten Raum.

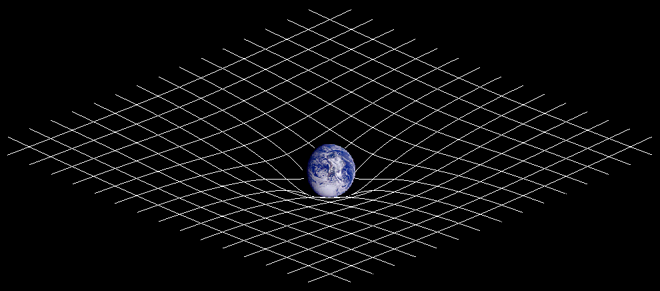
Das vernachlässigt natürlich, dass nicht nur der Raum beeinflusst wird, sondern auch die Zeit. In der Nähe von großen Massen vergeht diese etwas langsamer als weiter davon entfernt. Dieser Effekt muss zum Beispiel bei GPS Satelliten mitberücksichtigt werden, da diese im Verhältnis zur Zeitmessung auf der Erde, aufgrund, unter anderem, dieses Effektes etwas vorgehen.

Etwas pointierter gesagt: Für einen Raumfahrer dessen Raumschiff im (beinahe) leeren Raum zwischen den Galaxien strandet vergeht die Zeit schneller als für seine Freunde auf einem Planeten.

Die Einsteinschen Feldgleichungen

Was beschreibt nun aber das Zusammenspiel von Raum, Zeit und Energie? Die grundlegenden Gleichungen hierzu findet sich in der allgemeinen Relativitätstheorie und sind unter dem Namen „Einsteinsche Feldgleichungen“ bekannt. Sie lassen sich täuschend einfach bequem in einer Zeile zusammenfassen:

\[R_{\mu \nu} – \frac{1}{2}R g_{\mu \nu} + \Lambda g_{\mu \nu} = \frac{8 \pi G}{c^4} T_{\mu \nu}\]

Links des Gleichheitszeichens finden sich die Eigenschaften der Raumzeit, mit $R_{\mu \nu}$ als dem Ricci-Krümmungstensor, $R$ der skalaren Krümmung, $\Lambda$ der kosmologischen Konstante und $g_{\mu \nu}$ der Metrik der Raumzeit. Interessiert ist man zumeist daran wie $g_{\mu \nu}$ beschaffen ist.

Der Term rechts des Gleichheitszeichens beschreibt nun alles, was eben Einfluss auf die linke Seite hat, also auf die Beschaffenheit der Raumzeit. Der sogenannte Energie-Impuls Tensor $T_{\mu \nu}$ beinhaltet die Dichte und den Fluss von Energie (durch EM Felder zum Beispiel) und Impuls in der Raumzeit.

Löst man die so entstehenden Gleichungen und erhält die Metrik, so kann zum Beispiel berechnet werden, wie der Weg eines Lichtstrahls durch diese Raumzeitkrümmung beeinflusst wird. Genau das verfolgte André Füzfa, Professor für Mathematik und Astrophysik an der Universität von Namur, in eine bestimmte Richtung weiter.

Das vorgeschlagene Experiment

Zuerst suchte er sich ein passendes Koordinatensystem in dem die Lösung der Gleichungen für das von ihm betrachtete Experiment etwas weniger kompliziert möglich ist. Sein Ansatz war numerisch zu berechnen, wie das Magnetfeld, das durch den Strom entsteht welcher durch eine spezielle Helmholtzspule fließt, die Raumzeit krümmt. Und dann war natürlich noch wichtig zu wissen, welche Auswirkungen dies auf einen Lichtstrahl hat den man durch den so entstehenden Bereich zusätzlich gekrümmter Raumzeit durchschickt. Denn dies ist eine relativ unkomplizierte Methode zur Messung der Krümmung.

Im Prinzip gibt es dabei zwei Möglichkeiten

• Die Wellenlänge des Lichtes ändert sich (Rotverschiebung) bei seinem Weg durch die gekrümmte Raumzeit.
• Der zurückgelegte Weg ist unterschiedlich, da das Licht einer gekrümmten Bahn folgen muss.

Alles natürlich verglichen mit einem Lichtstrahl der einen Bereich der Raumzeit durchquert welcher nicht zusätzlich gekrümmt wird.

Die Ergebnisse legten nun Nahe, dass ersteres eher nicht messbar sein würde, zweiteres aber – mit einem sehr sensiblen Aufbau – eventuell schon.

Die Krümmung der Raumzeit wäre jedenfalls sehr klein, selbst wenn das Magnetfeld durch einen Strom von $I=2\cdot 10^4\;\text{A}$ in supraleitenden Spulen erzeugt würde (etwa das $20\;000$-fache von dem, was ein Handyladegerät an Strom zur Akkuladung liefern kann).

Kleine Unterschiede in der Weglänge können allerdings mit Interferometern sehr genau bestimmt werden: Der Laserstrahl trifft zunächst auf einen Strahlteiler auf welcher 50% des Lichts in die gekrümmte Raumzeit zwischen den Spulen umleitet, und 50% in einen unbeeinflussten Bereich. Auf dem Rückweg aus den jeweiligen Teilen werden die Lichtstrahlen wieder überlagert und auf diese Art und Weise verglichen. Hat einer einen etwas längeren oder kürzeren Weg zurückgelegt, verstärken sich die beiden Lichstrahlen oder schwächen sich, aufgrund der Phasendifferenz, ab. Eine Änderung in der Lichtintensität die ein Detektor feststellen kann! Den Begriff Phasendifferenz haben wir bereits in einem Artikel über das zerstörungsfreie Lesen alter Schriftrollen kennengelernt.

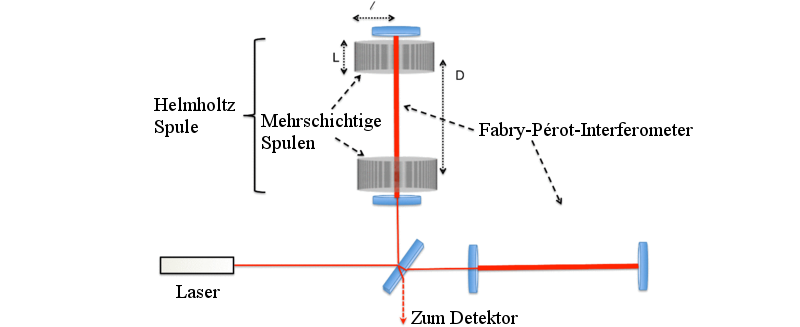
Nun, leider ist die Phasendifferenz aber nicht groß genug um messbar zu sein wenn man das Experiment nur kurz laufen lässt. Der Phasenschub, den grünes Laserlicht mit $514\;\text{nm}$ durch den verkürzten Weg im Bereich der gekrümmten Raumzeit zwischen den Spulen erfährt, beträgt, bei einmaligem Durchlauf, nur $\Delta \phi=-1.56\cdot 10^{-25}$. Zur Zeit ist das nicht messbar, selbst für ein Interferometer nicht. Aber durch die stehende Welle die sich im Fabry-Pérot-Interferometer ausbildet (das „festhalten“ des Lichts zwischen den Spiegeln), summiert sich dieser Phasenschub auf. Nach 200 Tagen ununterbrochenen Messens wäre schließlich ein $\Delta \phi$ in feststellbarer Größenordnung erreicht!

Natürlich weißt Füzfa selbst darauf hin, dass er nur zeigen möchte, dass aktuelle Technologie prinzipiell dazu fähig wäre, einerseits eine messbare Krümmung der Raumzeit zu generieren, und andererseits, diese dann auch messen zu können.

Prinzipiell ist dabei immer ein spannendes Wort, denn es zeigt, dass etwas zumindest rechnerisch machbar wäre. Es versteckt aber elegant die praktischen Schwierigkeiten die sich in der experimentellen Umsetzung ergeben. (zB. eliminieren von Vibrationen, thermische Ausdehnung/Schrumpfung des Messapparates, etc.)

Allerdings kann dieses Paper einem Experimentator irgendwo die nötige Zuversicht geben, dass die experimentellen Unwegsamkeiten überwindbar sind. Wer weiß, vielleicht wird die Raumzeit schon in naher/mittelferner Zukunft mit einem Magnetfeld gekrümmt und dies durch Messungen bestätigt.

Referenzen

Füzfa, André – „How current loops and solenoids curve space-time.“ in Physical Review D, 93, 024014, 2016.