Schrödingers Katze ist inzwischen den meisten ein Begriff. Doch was versteckt sich wirklich hinter diesem Gedankenexperiment? Was sollte damit aufgezeigt werden? Damit werden wir uns in diesem Artikel befassen. Wir starten mit den Axiomen der Quantenmechanik – den grundlegenden Annahmen der Theorie – und sehen uns an was diese besagen. Einerseits um eine bessere Idee von einer der am besten bestätigten Theorien unsrer Zeit zu bekommen, und andererseits um eine Grundlage für weitere Quantenmechanikartikel zu haben. Dafür werden wir uns etwas Zeit nehmen. Sobald wir das getan haben stoßen wir dann auf ein Paradoxon und nicht intuitive Folgen, und letzteres ist eben das was Schrödinger mit seiner Katze veranschaulicht hat.

Schrödingers Katze

Ein paar Worte vorweg

Dieser Artikel hat etwas länger gedauert. Ich habe mir viel Zeit mit den Formulierungen gelassen und hoffe, dass die Veranschaulichungen nicht übers Ziel hinausgeschossen sind und zu viel Raum für Ungenauigkeiten lassen. Das Problem ist, dass jedes anschauliche Bild sich mehr oder weniger alltäglicher Objekte bedienen muss und schon allein dadurch eine Diskrepanz zum quantenmechanischen Phänomen entsteht. Wie sich etwas verhält wird durch Gleichungen und nicht Erzählungen und Analogien beschrieben. Anschauliche Beispiele können manche Aspekte näherungsweise wiedergeben, aber in anderen vollkommen versagen. Das sollte man an den entsprechenden Stellen im Hinterkopf behalten.

Ganz ohne Gleichungen ging es nicht und wollte ich das Thema auch nicht behandeln. Wo welche vorkommen versuche ich auch in Worten zu erklären was passiert, und für Interessierte gibt es wie auch sonst die Möglichkeit sich über die ausklappbaren Boxen etwas mehr Details zu beschaffen. Grundsätzlich hatte ich auch die Möglichkeit mich zwischen zwei Notationsarten zu entscheiden – namentlich zwischen „klassischer“ und Braket- bzw. Diracnotation. Ich habe mich für eine Mischung aus beiden entschieden. Während die Braket Notation sich auf das wesentliche beschränkt fand ich es ganz nützlich zumindest anfangs die Integrale auszuschreiben.

Nachdem das Thema auch sehr umfangreich ist streifen wir viele andere interessante Fragestellungen (das Messproblem, Verschränkung und das EPR Paradoxon, das Doppelspaltexperiment, …) hier nur am Rande – aber irgendwann bekommen die ihre eigenen Artikel.

Die Grundlagen der Quantenmechanik

Beginnen wir am Anfang. Wie auch die Newtonsche Mechanik, so hat auch die Quantenmechanik drei grundlegende Axiome auf denen das Theoriegebäude aufbaut. Es gibt keine grundlegenderen Regeln oder Annahmen, alles weitere leitet sich aus diesen Axiomen ab. Schreiben wir sie erstmal zusammengefasst auf, und dann versuchen wir sie etwas anschaulicher zu betrachten und uns Gedanken darüber zu machen.

1. Der Zustand eines Systems wird vollständig durch eine Wellenfunktion $\Psi$ beschrieben.
2. Wie sich das System mit der Zeit verändert sagt uns die Schrödinger Gleichung
3. Eine Messung reduziert die Wellenfunktion auf einen Eigenzustand des Messoperators.

Zugegeben, das klingt auf den ersten Blick etwas weniger verständlich als die Newtonschen Axiome. Bringen wir etwas Licht in die Sache und versuchen das etwas anschaulicher zu formulieren.

Das erste Axiom

Der Zustand eines Systems wird vollständig durch eine Wellenfunktion $\Psi$ beschrieben.

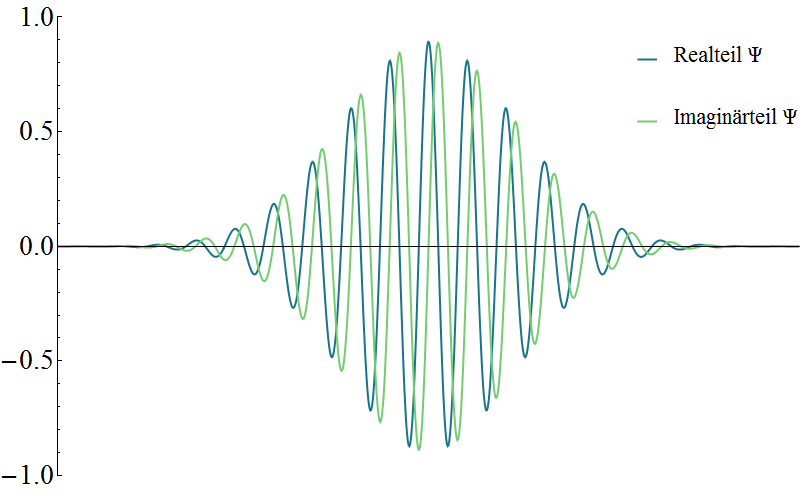
Quantenmechanisch beschreiben wir etwas mit einer Wellenfunktion, diese wird oft mit dem griechischen Buchstaben Psi ($\Psi$ oder $\psi$) bezeichnet. Können wir diese angeben dann sagt uns dies alles was wir über das Objekt das wir beschreiben wissen können und alles was es darüber zu wissen gibt. Die Beschreibung durch die Wellenfunktion ist vollständig. Es gibt verschiedene Möglichkeiten wie der Zustand schließlich genau notiert wird – als Funktion $\Psi$ in Abhängigkeit von bestimmten Koordinaten oder in Dirac Notation als Brakets $\langle \Psi |$ (Bra) und $| \Psi \rangle$ (Ket) welche Vektoren in einem Hilbertraum darstellen. Das ist ein spezieller mathematischer Raum in welchem es Objekte (Vektoren) gibt, für die bestimmte mathematische Operationen definiert sind.

Die Sache mit den Wahrscheinlichkeiten

Aber was kann man sich darunter vorstellen? Das ist tatsächlich noch eine vieldiskutierte Frage. Denn die Wellenfunktion liefert komplexe Zahlen als Ergebnis, aber alle Messungen die wir durchführen könnten haben reelle Zahlen als Ergebnis (Ortskoordinate und Geschwindigkeit zum Beispiel). Gibt es also irgendetwas in der tatsächlichen Welt, dass dieser Funktion entspricht? Hierzu gibt es verschiedene Interpretationsmodelle, wie zum Beispiel die Kopenhagener Deutung der Quantenmechanik. Welches die passendste Interpretation oder Deutung ist, ist Gegenstand der aktuellen Forschung.

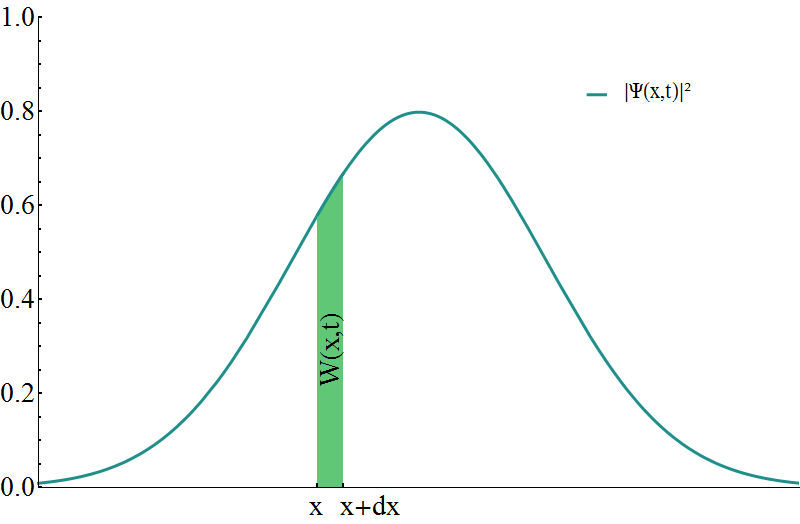
Einen direkten Bezug zu messbaren Größen erhält die Wellenfunktion $\Psi$ jedenfalls dann wenn wir ihr Absolutquadrat $|\Psi(x,t)|^2$ bilden und uns einen Ausschnitt des Raumes der Breite $\Delta x$ ansehen:

\[ W(x,t,\Delta x) \approx\left| \Psi(x,t) \right|^2\;\Delta x\]

Nach dieser Operation erhalten wir schließlich nur mehr reelle Zahlen. Der Ausdruck oben beschreibt die Wahrscheinlichkeit ein Teilchen zum Zeitpunkt $t$ im Bereich $x$ bis $x+\Delta x$ aufzufinden. Um so kleiner der Ausschnitt gewählt wird, um so exakter ist diese Rechnung. (Das führt in weiterer Folge auf ein Integral – etwas mehr dazu in der ausklappbaren Box). Das ist auch bereits ein großer Unterschied zur klassischen Physik – in dieser können wir nämlich, wenn wir von einem System alle möglichen Parameter kennen (was dort prinzipiell möglich ist), exakt mit Wahrscheinlichkeit $1$ vorhersagen in was für einem Zustand es sich zu jedem beliebigen Zeitpunkt befindet. Zum Beispiel wissen wir, wenn ein Stein in eine bestimmte Richtung geworfen wird, klassisch genau welche Bahn er beschreiben wird.

Ist der Winkel unter dem der Stein geworfen wurde bekannt, sowie die Geschwindigkeit wenn er die Wurfhand verlässt so lässt sich die Wurfbahn genau berechnen. Natürlich ließe sich diese Situation beliebig verkomplizieren, zum Beispiel durch Luftwiderstand, Wind und so weiter, allerdings ändert dies nichts daran, dass wir in der klassischen Physik prinzipiell alle diese Größen kennen könnten und somit in unseren Berechnungen berücksichtigen könnten. Wir können also grundsätzlich die Bahn immer noch exakt vorhersagen.

Grenzen der Genauigkeit

Nicht so in der Quantenmechanik: Für den Ausgang eines Experimentes können hier nur mehr Wahrscheinlichkeiten angegeben werden. Mehr noch, sogar der Möglichkeit alle Parameter des Systems genau zu kennen werden durch die Heisenbergsche Unschärferelation Grenzen gesetzt. Bestimmte Größen welche zueinander komplementär sind können nicht gleichzeitig beliebig genau bekannt sein. Ort und Impuls einen Teilchens sind dafür ein beliebtes Beispiel. Das Produkt ihrer Orts- und Impulsunschärfe ist immer

\[ \Delta x \Delta p \geq \frac{\hbar}{2} \]

Das ist aber noch nicht alles. Es geht nicht nur darum, dass wir diese Größen nicht genau kennen können weil unsere Messgeräte nicht genau genug sind. Die Aussage ist viel fundamentaler! Vor der Messung gibt es schlichtweg keinen wahren oder tatsächlichen Wert. Es gibt auch keinen versteckten Parameter der diesen bei einer Messung dann festlegt, es ist eine tiefgehende Unschärfe die sich nicht durch noch so gefinkelte Messgeräte und -verfahren loswerden lässt. Aber das würde an dieser Stelle zu weit führen, genauere Überlegungen diesbezüglich werden wir in einem Artikel über das EPR Paradoxon weiter verfolgen. Dieses Paper von Einstein, Podolski und Rosen (daher der Name EPR) beschäftigt sich nämlich unter anderem genau mit den Folgen die sich daraus ergeben.

[expand title=“Wahrscheinlichkeiten und Wahrscheinlichkeitsdichten“]

Exakt müssen wir von Wahrscheinlichkeitsdichten $w(x,t)$ sprechen wenn wir nur das Absolutquadrat der Wellenfunktion bilden. Dieses ist gegeben durch

\[|\Psi(x,t)|^2=\Psi^*(x,t)\Psi(x,t)\]

wobei $\Psi^*(x,t)$ für die komplexe Konjugation der ursprünglichen Wellenfunktion steht. Die Wahrscheinlichkeit ein Teilchen in einem Raumbereich $\Delta x$ um einen Ort $x$ vorzufinden erhalten wir schließlich erst durch Integration über diesen Raumbereich:

\[ W(x,t,\Delta x) = \int\limits_{x}^{x+\Delta x} \left|\Psi(x‘,t) \right|^2 \; dx‘ \]

Für exakt einen Ort $x$ mit $\Delta x=0$ ergibt sich damit also $W(x,t)=0$. Das macht ja auch Sinn, denn ein Ort genau entspricht ja einem infinitesimal kleinen Abschnitt des Raumes, und da es unendlich viele andere gleich schmale Raumbereiche gibt ist die Wahrscheinlichkeit ein Teilchen genau in diesem einen zu finden gleich Null.

Die Wahrscheinlichkeit das System irgendwo im Raum zu finden ist natürlich zu jedem Zeitpunkt $1$.

\[ W(t) = \int\limits_{-\infty}^{\infty} |\Psi(x,t)|^2\; dx\]

Das weißt auch darauf hin, dass Wellenfunktionen immer normiert sind.

[/expand]

Das zweite Axiom

Wie sich das System mit der Zeit verändert sagt uns die Schrödinger Gleichung

So wie in der klassischen Physik Kräfte bedingen wie der Impuls eines Objektes sich mit der Zeit ändert, und somit dessen Position (2. Newtonsches Axiom), so gibt es in der Quantenmechanik die Schrödingergleichung welche uns sagt wie sich die Wellenfunktion mit der Zeit verändert:

\[ i\hbar \frac{\partial}{\partial t} \Psi(x,t)= H\Psi(x,t)\]

mit $i$ als Imaginärer Zahl und $\hbar$ dem Planck’schen Wirkungsquantum durch $2 \pi$ dividiert. Folgendes steht eigentlich da: Die zeitliche Änderung der Wellenfunktion (linke Seite der Gleichung) hängt zusammen mit der Gesamtenergie des beschriebenen Systems (rechte Seite). Das $H$ rechts steht dabei für den Hamilton Operator welcher aus Termen besteht welche eben jene Gesamtenergie ergeben. Also zum Beispiel die Summe aus kinetischer und potentielle Energie.

[expand title=“Ein typischer Hamilton Operator…“]
…wäre zum Beispiel
\[ H = -\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2} + V(x,t) \]
Der erste Term entspricht der kinetischen Energie, der zweite einem Potential – zum Beispiel verursacht durch ein elektrisches Feld.
[/expand]

Die Zeitentwicklung

Diese so beschriebene Veränderung ist kontinuierlich und stetig, es ist für jeden beliebigen Zeitpunkt bekannt wie die Wellenfunktion aussieht. Es treten keine Sprünge auf. Die zeitliche Entwicklung der Wahrscheinlichkeitsdichte eines Teilchens sähe zum Beispiel so wie in der folgenden Abbildung gezeigt aus:

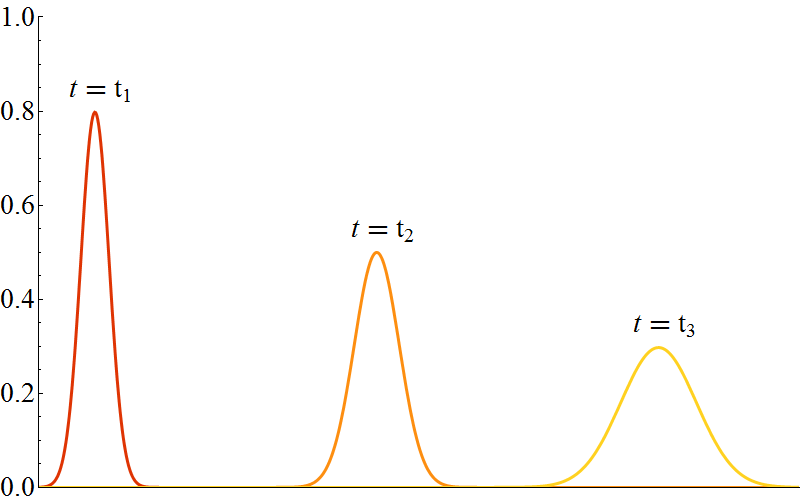
Anschaulich kann man sich vorstellen, dass wir ein Teilchen beschreiben welches klassisch eine gewisse Geschwindigkeit $v$ hat. Zum Zeitpunkt $t_1$ ist die Wahrscheinlichkeit es am Ursprung zu finden am höchsten, zum Zeitpunkt $t_2$ ist die Wahrscheinlichkeit es am Ort $v \cdot (t_2 – t_1)$ zu finden am größten. Ganz so wie man es für ein gleichmäßig bewegtes Teilchen erwarten würde.

Ein wichtiger Punkt der durch obige Grafik nicht vollständig vermittelt werden kann ist, dass die Entwicklung kontinuierlich erfolgt. Die folgende Animation soll dies etwas besser veranschaulichen und damit sichs besser zeigen lässt bewegen wir uns quasi mit dem Teilchen mit. Der einzige Sprung der auftritt ist, wenn die Animation neu startet nachdem wir das Auseinanderfließen bis zu einem bestimmten Zeitpunkt mitverfolgt haben. Tatsächlich würde es sich noch unendlich lange fortsetzen solange keine Messung durchgeführt wird:

Die Verbreiterung bzw. die zunehmende Unsicherheit wo sich das Teilchen denn genau befindet ist auch als Auseinanderfließen des Wellenpaketes bekannt. Darunter versteht man die in der Animation oben sichtbare Verbreiterung des Wellenpaketes.

Superpositionen

Eine weitere spannende Eigenschaft ergibt sich daraus, dass die Schrödingergleichung eine lineare partielle Differentialgleichung ist. Das bedeutet, dass wenn wir zwei Wellenfunktionen $\Psi_1$ und $\Psi_2$ gefunden haben die beide jeweils Lösungen sind, dann ist auch ihre Summe $\Psi_1 + \Psi_2$ eine Lösung. Das führt zu einem als Überlagerung oder Superposition bekanntem Phänomen – ein quantenmechanisches System kann aus einer Überlagerung von Zuständen bestehen. Dazu kommen wir aber später nochmal genauer, denn dies wird ein wichtiger Punkt bei Schrödingers Katze sein.

Das dritte Axiom

Eine Messung reduziert die Wellenfunktion auf einen Eigenzustand des Messoperators.

Alles was wir an einem System nun messen können ist – etwas anders formuliert – für uns beobachtbar. Diese Größen sind sogenannte Oberservablen und werden mathematisch gesehen durch Operatoren repräsentiert.

Zwei sehr bekannte Beispiele für Observablen bzw. den ihnen entsprechenden Operatoren sind der Ort $x$ eines System und dessen Impuls $p$, wobei die Operatoren oft durch die jeweiligen Großbuchstaben gekennzeichnet werden.

Folgendermaßen sehen Orts- und Impulsoperator im Ortsraum aus:

\[ X = x \]

bzw. der Impulsoperator

\[ P = -i \hbar \frac{\partial}{\partial x}\]

Aber was kann man nun damit machen? Nun, wir können im Formalismus der Quantenmechanik zum Beispiel die folgenden beiden Fragen stellen:

• Was ist das wahrscheinlichste Ergebnis wenn ich in einem Experiment eine Observable messe? (Erwartungswert)
• Wie wahrscheinlich ist es, das System nach einer Messung in einem bestimmten Zustand vorzufinden? (Übergangsamplitude)

Für zweiteren Punkt benötigen wir eigentlich keine Operatoren aber es bietet sich an, es dennoch an dieser Stelle mit zu betrachten.

Beides sind jedenfalls für eine Theorie immens wichtige Bestandteile! Auf irgendeine Art und Weise wollen wir ja Mechanismen zur Hand haben mit welchen sich Vorhersagen tätigen lassen.

Führen wir an einem quantenmechanischen System nun eine Messung durch, welches sich im Zustand $\Psi$ befindet, so finden wir es nach der Messung in einem Zustand $\Phi$ (Phi) vor. Dieser neue Zustand ist schließlich ein Eigenzustand des Messoperators, wobei in weiterer Folge nicht so wichtig ist, was das spezielle an einem Eigenzustand ist (die Box unterhalb hat aber auch dazu was zu sagen).

[expand title=“Erwartungswerte, Eigenzustände und Übergangsamplituden“]

Wir haben also wieder unser System das wir durch eine Wellenfunktion $\Psi$ beschreiben. Wollen wir nun für einen bestimmten Zeitpunkt $t$ wissen, wo wir es bei einer Messung am wahrscheinlichsten finden werden, also die erste von den beiden Fragen stellen und den Ortsoperator Erwartungswert $X_\Psi$ bestimmen, müssen wir folgendes Integral auswerten:

\[ X_\Psi = \int\limits_{-\infty}^{\infty} \Psi^*(x,t) \; X \; \Psi(x,t) \; dx\]

Dies liefert den sogenannten Erwartungswert eines Operators – das wahrscheinlichste Ergebnis einer Messung.

Wenn wir aber wissen möchten wie wahrscheinlich es ist das System nach der Messung in einem bestimmten Zustand $\Phi$ zu finden, also ein bestimmtes Ergebnis vorzufinden, sieht das Integral etwas anders aus:

\[\int\limits_{-\infty}^{\infty} \Phi^*(x,t) \; \Psi(x,t) \; dx\]

Diese Größe wird Übergangsamplitude genannt und ihr Absolutquadrat gibt an, wie wahrscheinlich es ist das System welches ursprünglich im Zustand $\Psi(x,t)$ war nach einer Messung im Zustand $\Phi(x,t)$ vorzufinden.

Was genau passiert quantenmechanisch betrachtet nun bei der Messung? Das Axiom sagt, dass die Wellenfunktion auf einen Eigenzustand des Messoperators reduziert wird. Gut, was ein Messoperator ist, darunter können wir uns jetzt schon etwas vorstellen. Sie ermöglichen es uns Wahrscheinlichkeiten für Messergebnisse anzugeben und es gibt zum Beispiel den Ortsoperator $X$ oder den Impulsoperator $P$. Was sind nun Eigenzustände?

Formal ist ein Eigenzustand $\psi$ eines Operators $A$ ein Zustand für den gilt:

\[A \psi = \alpha \psi \]

wobei $\alpha$ eine reelle Zahl ist. Angenommen wir haben ein System im Eigenzustand $\psi$ eines Operators $A$ vorliegen. Was ist der Erwartungswert von $A$?

Diesen ermitteln wir nun – zum Beispiel für eine Wellenfunktion im Ortsraum – wieder über folgendes Integral, nur können wir diesmal etwas umformen:

\[ \int\limits \psi(x)^*\; A \;\psi(x) \; da= \int \psi(x)^* \;\alpha\;\psi(x)\;dx\]

Hier haben wir einfach die Eingangs gezeigte definierende Eigenschaft des Eigenzustandes verwendet.

Da $\alpha$ nicht von der Integrationsvariable abhängt können wir es vor das Integral ziehen, was übrig bleibt ist

\[ \alpha \int \psi(x)^* \; \psi(x) \; dx = \alpha \int |\psi(x)|^2 dx\]

und da Wellenfunktionen auf den jeweiligen Definitionsbereichen normiert sind ist immer $\int|\psi(x)|^2\;da=1$. Also ist das Ergebnis für den Erwartungswert $A_\psi$ von $A$:

\[A_\psi = \alpha \]

Etwas ausführlicher wird diese Thema im Demtröder – Experimentalphysik 3 im Kapitel Grundlagen der Quantenmechanik behandelt!

[/expand]

Wie genau aus $\Psi$ der Zustand $\Phi$ wird, darüber sagen die Axiome nichts aus. Der Übergang ist sprunghaft oder diskontinuierlich, oft wird hier von einer Reduktion des Wellenpaketes, oder blumiger, von einem Kollaps desselben gesprochen. Vorstellen, sofern das möglich ist, kann man sich das aus Experimentatorensicht so:

Angenommen wir haben eine große absolut dunkle und kalte leere Box innerhalb deren Vakuum sich ein einziges Teilchen befindet. Wir wissen nur, dass wir das Teilchen (wie auch immer) irgendwann etwa in der Mitte der Box eingebracht haben. Mit fortschreitender Zeit fließt das Wellenpaket mit dem wir das Objekt beschreiben immer weiter auseinander, die Wahrscheinlichkeit es auch abseits von der Mitte zu finden wird größer, während die Wahrscheinlichkeit es genau in der Mitte zu finden schrumpft.

Jetzt leuchten wir in die Box hinein und irgendwo werden wir, zum Beispiel aufgrund von Rayleigh Streuung, etwas das zurückleuchtet wahrnehmen – und zwar an der Stelle, wo sich das Teilchen befindet. Bevor wir gemessen haben hatten wir ein Wellenpaket welches schon etwas auseinandergeflossen war – das Teilchen hatte keine exakte Position. Erst durch die Messung reduziert sich dieses bereits verbreiterte ursprüngliche Wellenpaket auf ein ganz schmales sehr stark lokalisiertes.

Genau hier stoßen wir auf ein interessantes Paradoxon, und von hier an werden wir auch die Dirac Notation verwenden um das Ganze etwas fokussierter zeigen zu können.

Überlagerungen im Mikrokosmos

Einerseits haben wir die kontinuierliche und deterministische zeitliche Entwicklung wo zu jedem Zeitpunkt der Zustand eines Systems genau bekannt ist. Andererseits ist die Veränderung durch den Messvorgang sprunghaft und ihr Ergebnis zufällig. Die Wahrscheinlichkeit jedes Ergebnisses kann vorhergesagt werden – wiederholen wir das Experiment also sehr oft dann merken wir, dass wir das Teilchen an bestimmten Positionen öfter finden als an anderen. Das können wir vorhersagen, aber nicht an welcher Position wir das Teilchen bei genau einem Experiment finden werden.

Dasselbe Experiment kann man sich nun auch mit einem radioaktiven Teilchen vorstellen, nehmen wir eines mit einer Halbwertszeit $\lambda$. Wenn wir mit einer großen Anzahl solcher Teilchen starten können wir vorhersagen, dass nach Ablauf der Halbwertszeit nur mehr etwa die Hälfte vorhanden sein wird. Aber was passiert, wenn wir nur ein einzelnes betrachten?

Beschreiben wir den Zustand $|\Psi\rangle$ des Systems quantenmechanisch dann beginnen wir mit einem Teilchen und diesen Zustand nennen wir $|1\rangle$. Um so mehr Zeit vergeht desto wahrscheinlicher wird es, dass dieses zerfallen ist – diesen Zustand bezeichnen wir mit $|0\rangle$. Solange wir nicht messen diktiert die Schrödingergleichung wie sich das System entwickelt. Allerdings können wir bereits ohne auf diese zurückzugreifen ein paar Sachen feststellen:

Je früher wir nachsehen desto wahrscheinlicher ist es, dass wir das Teilchen noch auffinden

\[ |\langle 0|\Psi\rangle|^2 \rightarrow 0\quad \text{bei}\; t \rightarrow 0 \]

\[ |\langle 1|\Psi\rangle|^2 \rightarrow 1\quad \text{bei}\; t \rightarrow 0 \]

aber um so länger wir uns Zeit lassen, desto wahrscheinlicher wird es, kein Teilchen mehr anzutreffen

\[ |\langle 0|\Psi\rangle|^2 \rightarrow 1\quad \text{bei}\; t \rightarrow \infty \]

\[ |\langle 1|\Psi\rangle|^2 \rightarrow 0\quad \text{bei}\; t \rightarrow \infty \]

Da die Halbwertszeit bekannt ist können wir sogar noch etwas mehr über unser System aussagen. Wenn wir genau zu $t=\lambda$ nachsehen dann ist die Wahrscheinlichkeit dafür, dass wir noch ein Teilchen vorfinden genauso hoch wie jene, dass es zerfallen ist:

\[|\langle 0|\Psi\rangle|^2 =|\langle 1|\Psi\rangle|^2 = 0.5 \]

Und somit wissen wir eigentlich schon ganz schön viel ohne überhaupt die Schrödingergleichung lösen zu müssen. Wir können sogar noch weitermachen da wir wissen, dass die Entwicklung kontinuierlich sein muss. Das bedeutet in diesem Fall, dass die Wahrscheinlichkeit das System im Zustand $|1\rangle$ (Teilchen da) anzutreffen zwar abnimmt, aber nie $0$ wird. Selbiges gilt mit umgekehrtem Vorzeichen dafür es im Zustand $|0\rangle$ (Teilchen weg) vorzufinden – diese Wahrscheinlichkeit nimmt zwar zu aber wird nie $1$. Beide Zustände müssen also immer im Gesamtsystem vorhanden sein – und hier liefert die Superpositionseigenschaft der Schrödingergleichung die Antwort.

Das Gesamtsystem befindet sich, solange wir nicht messen, in einer Überlagerung aus zwei Zuständen

\[ |\Psi\rangle = a|0\rangle + b|1\rangle \]

Das Teilchen ist, im quantenmechanischen Formalismus, gleichzeitig vorhanden und zerfallen. Sobald wir messen reduziert sich die Zustandsfunktion des Systems auf einen der beiden Zustände und wir stellen entweder den einen oder den anderen Zustand fest. Führen wir eine Reihe an Experimenten durch und zählen wie oft wir zur Halbwertszeit das Teilchen noch vorfinden, dann würden wir erwarten, dass dies in etwa bei der Hälfte aller Experimente so ist.

Schrödinger war durchaus bewusst, dass sich daraus seltsame Konsequenzen ergeben:

Man kann auch ganz burleske Fälle konstruieren.

Erwin Schrödinger, 1935

Aber wie demonstriert man das am eindrucksvollsten?

Die Katze betritt die Bühne / Box

Grundsätzlich gelten die Axiome der Quantenmechanik für alle Objekte der Welt. Angefangen von kleinsten Elementarteilchen bis hin zu beliebiger Größe. Darüber wo die Gültigkeitsgrenzen dieser Theorie liegen wird aktuell viel geforscht.

Aber könnte man mit einem schlauen experimentellen Aufbau eine Superposition für ein Objekt alltäglicher Größe erzwingen?

Stellen wir uns eine absolut leere Box vor die ihr inneres vollkommen von der Aussenwelt abschirmt. Wir fügen ihr die folgenden Dinge hinzu: Eine Katze, ein radioaktives Teilchen, einen Geigerzähler, einen Mechanismus an den ein Hammer angebracht ist, und, um bei Schrödingers ursprünglichem Setup zu bleiben, ein Kölbchen Blausäure. Das Funktionsprinzip des Mechanismus soll so sein, dass dieser, sobald der Geigerzähler einen Zerfall feststellt, mit dem Hammer den Blausäurekolben zerbricht. Dies setzt das Gift frei welches die Katze umbringt. Nachdem alles drinnen ist schließen wir die Box.

Was wir nun erreicht haben ist, dass wir den Zustand der Katze mit dem quantenmechanischen Zustand des radioaktiven Teilchens verknüpft haben – den Mikro- mit dem Makrokosmos. Das Wohlergehen der Katze (ihr Zustand) hängt nun direkt mit dem Zustand des Teilchens zusammen! Der Zustand des Gesamtsystems in der Box ist

\[ |\Psi\rangle =c|0\;\text{und}\;\text{Katze}_\text{tot}\rangle\ + d|1\;\text{und}\;\text{Katze}_\text{lebt}\rangle\]

Eine exaktere Formulierung finden interessierte zum Beispiel bei Legett (2002).

Was passiert nun also, wenn wir wieder zur Halbwertszeit $\lambda$ die Box öffnen und nachsehen? Wieder werden wir entweder die eine oder die andere Situation realisiert vorfinden – entweder die Katze lebt oder sie ist verstorben. Und wir würden – wenn wir das Experiment trotz der ethischen Probleme sehr oft durchführen – in etwa in der Hälfte der Fälle erwarten eine lebende Katze zu bergen. Um so früher wir nachsehen um so mehr Katzen werden die Experimente überleben, je später desto ungünstiger.

Man kann nun wieder die berechtigte Frage stellen was denn in der Box vor sich geht bevor wir sie öffnen und genau da wirds interessant. Denn es ist nun einmal so, dass die Quantenmechanik zu den am bestbestätigsten Theorien unserer Zeit gehört – ihre Vorhersagen sind also ernst zu nehmen. Aber wie ist es mit der Wellenfunktion, hat diese also eine Entsprechung in der Wirklichkeit? Ein Ja würde bedeuten, dass es Katzen gäbe die lebendig und tot gleichzeitig sind, ein Nein wirft die Frage nach der Interpretation der Theorie auf. Was ist diese Wellenfunktion und warum sollte es nicht, so wie bei Kräften in der Newtonschen Mechanik, ein Gegenstück in der Realität geben?

Tatsächlich gibt es Argumente die dafür und dagegen sprechen, und beide sind nicht vollständig befriedigend (siehe zum Beispiel Leggett (2005)). Es gibt auch den Standpunkt, dass auf dem Weg zur Alltagswelt irgendwo Prozesse (wie zum Beispiel Dekohärenz) einsetzen welche Superpositionen (wie die Katze die tot und lebendig gleichzeitig ist) auflösen und daher verhindern, dass wir eine Katze in einem Überlagerungszustand halten können.

Das Gedankenexperiment Schrödingers Katze ist eng verwoben mit den Grundlagen der Quantenmechanik und damit verbundenen Fragestellungen wie dem Messproblem. Bricht der quantenmechanische Formalismus auf dem Weg von subatomaren Teilchen bis hin zur Alltagsgröße irgendwann zusammen? Gibt es einen Mechanismus der Überlagerungen ab einer bestimmten Grenze verhindert? Die aktuelle Forschung ist in diesem Bereich höchst aktiv und spannend.

In diesem Artikel hatten wir wenn es um den Mikrokosmos ging immer von einem einzelnen Teilchen gesprochen wenn es um Zustände und deren Zeitentwicklung ging. Tatsächlich wurde aber auch bereits für Moleküle mit über $10\;000\text{u}$ (Atommassenzahlen) gezeigt, dass dieser Formalismus immer noch gültig ist (Eibenberger 2013)! Dies entspricht dem Gewicht von etwas mehr als $10\;000$ Wasserstoffatomen oder, anders formuliert, diese Moleküle bestehen aus etwa $5000$ Protonen, $5000$ Neutronen und $5000$ Elektronen. DAS ist schon ein ganzes Stück weg von kleinen einzelnen Elementarteilchen. Ob es also eine prinzipielle Schranke gibt, ab welche quantenmechanische Vorhersagen nicht mehr gültig sind bleibt spannend! Im Moment wird versucht genau dies auszuloten und irgendwann werden Experimente wie diese eine Antwort auf die Frage liefern, ob Schrödingers Katze gleichzeitig tot oder lebendig ist.

Danksagung

Mein Dank gilt…

• Julia Gingras für Animation und Titelbild-Illustration! Auf ihrer Homepage gibt es mehr von ihren Werken zu sehen!
• Harald Ringbauer für Diskussion und fachliches Feedback.

Literatur

Demtröder – Experimentalphysik 3, Atome, Moleküle und Festkörper.

Schrödinger, Erwin. Die gegenwärtige Situation in der Quantenmechanik. Naturwissenschaften, 1935, 23.49, 823-828.

Leggett, A. J. Testing the limits of quantum mechanics: motivation, state of play, prospects. Journal of Physics: Condensed Matter, 2002, 14:R415-R451.

Leggett, A. J. The quantum measurement problem. Science, 2005, 307:871.

Eibenberger, Sandra, et al. Matter–wave interference of particles selected from a molecular library with masses exceeding 10000 amu. Physical Chemistry Chemical Physics, 2013, 15.35, 14696-14700.